
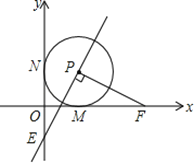
ЁОЬтФПЁПвбжЊдкЦНУцжБНЧзјБъЯЕxOyжаЃЌOЪЧзјБъдЕуЃЌвдPЃЈ1ЃЌ1ЃЉЮЊдВаФЕФЁбPгыxжсЁЂyжсЗжБ№ЯрЧагкЕуMКЭЕуNЃЌЕуFДгЕуMГіЗЂЃЌбиxжсе§ЗНЯђвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌСЌНгPFЃЌЙ§ЕуPзїPEЁЭPFНЛyжсгкЕуEЃЌЩшЕуFдЫЖЏЕФЪБМфЪЧtУыЃЈtЃО0ЃЉ
ЃЈ1ЃЉШєЕуEдкyжсЕФИКАыжсЩЯЃЈШчЭМЫљЪОЃЉЃЌЧѓжЄЃКPE=PFЃЛ
ЃЈ2ЃЉдкЕуFдЫЖЏЙ§ГЬжаЃЌЩшOE=aЃЌOF=bЃЌЪдгУКЌaЕФДњЪ§ЪНБэЪОbЃЛ
ЃЈ3ЃЉзїЕуFЙигкЕуMЕФЖдГЦЕуFЁфЃЌОЙ§MЁЂEКЭFЁфШ§ЕуЕФХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуQЃЌСЌНгQEЃЎдкЕуFдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЃЌЪЙЕУвдЕуQЁЂOЁЂEЮЊЖЅЕуЕФШ§НЧаЮгывдЕуPЁЂMЁЂFЮЊЖЅЕуЕФШ§НЧаЮЯрЫЦЃПШєДцдкЃЌЧыжБНгаДГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)ЁЂжЄУїЙ§ГЬМћНтЮіЃЛ(2)ЁЂb=2+aЛђb=2ЃaЃЛ(3)ЁЂt=![]() ЃЌt=
ЃЌt=![]() ЃЌt=2ЁР
ЃЌt=2ЁР![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)ЁЂСЌНгPMЁЂPNЃЌИљОнЧаЯпЕФаджЪЕУГіPM=PNЃЌИљОнОЭNPM=ЁЯEPF=90ЁуЕУГіЁЯNPE=ЁЯMPFЃЌДгЖјЫЕУїЁїPMFКЭЁїPNEШЋЕШЃЌДгЖјЫЕУїPE=PFЃЛ(2)ЁЂИљОнtЃО1КЭ1ЃМtЁм1СНжжЧщПіЧѓГіaКЭbЕФЙиЯЕЃЛ(3)ЁЂИљОнЯрЫЦШ§НЧаЮЕФМИжжВЛЭЌЕФЧщПіЧѓГіtЕФжЕ.
ЪдЬтНтЮіЃК(1)ЁЂШчЭМЃЌСЌНгPMЃЌPNЃЌ
ЁпЁбPгыxжсЃЌyжсЗжБ№ЯрЧагкЕуMКЭЕуNЃЌ ЁрPMЁЭMFЃЌPNЁЭONЧвPM=PNЃЌ
ЁрЁЯPMF=ЁЯPNE=90ЁуЧвЁЯNPM=90ЁуЃЌЁпPEЁЭPFЃЌ ЁЯNPE=ЁЯMPF=90ЁуЉЁЯMPEЃЌ
дкЁїPMFКЭЁїPNEжаЃЌЁЯNPE=ЁЯMPF PN=PM ЁЯPNE=ЁЯPMF ЃЌЁрЁїPMFЁеЁїPNEЃЈASAЃЉ ЁрPE=PFЃЌ
(2)ЁЂНтЃКЂйЕБtЃО1ЪБЃЌЕуEдкyжсЕФИКАыжсЩЯЃЌ
гЩЃЈ1ЃЉЕУЁїPMFЁеЁїPNEЃЌЁрNE=MF=tЃЌPM=PN=1ЃЌ Ёрb=OF=OM+MF=1+tЃЌa=NEЉON=tЉ1ЃЌ
ЁрbЉa=1+tЉЃЈtЉ1ЃЉ=2ЃЌЁрb=2+aЃЌ
Ђк0ЃМtЁм1ЪБЃЌШчЭМ2ЃЌЕуEдкyжсЕФе§АыжсЛђдЕуЩЯЃЌ
ЭЌРэПЩжЄЁїPMFЁеЁїPNEЃЌ Ёрb=OF=OM+MF=1+tЃЌa=ONЉNE=1ЉtЃЌ Ёрb+a=1+t+1Љt=2ЃЌ Ёрb=2ЃaЃЌ
(3)ЁЂt=![]() ЃЌt=
ЃЌt=![]() ЃЌt=2ЁР
ЃЌt=2ЁР![]()


 ЭѕКѓалбЇАИНЬВФЭъШЋНтЖСЯЕСаД№АИ
ЭѕКѓалбЇАИНЬВФЭъШЋНтЖСЯЕСаД№АИ КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ
КЃЕэПЮЪБаТзївЕН№АёОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНсКЯЪ§жсгыОјЖджЕЕФжЊЪЖЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЪ§жсЩЯБэЪО4КЭ1ЕФСНЕужЎМфЕФОрРыЪЧЁЁ ЁЁЃЛБэЪОЉ3КЭ2СНЕужЎМфЕФОрРыЪЧЁЁ ЁЁЃЛвЛАуЕиЃЌЪ§жсЩЯБэЪОЪ§mКЭЪ§nЕФСНЕужЎМфЕФОрРыЕШгк|mЉn|ЃЎШчЙћБэЪОЪ§aКЭЉ2ЕФСНЕужЎМфЕФОрРыЪЧ3ЃЌФЧУДaЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєЪ§жсЩЯБэЪОЪ§aЕФЕуЮЛгкЉ4гы2жЎМфЃЌЧѓ|a+4|+|aЉ2|ЕФжЕЃЛ
ЃЈ3ЃЉЕБaШЁКЮжЕЪБЃЌ|a+5|+|aЉ1|+|aЉ4|ЕФжЕзюаЁЃЌзюаЁжЕЪЧЖрЩйЃПЧыЫЕУїРэгЩЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮ ![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп ![]() ЗжБ№гыЯпЖЮ
ЗжБ№гыЯпЖЮ ![]() НЛгкЕу
НЛгкЕу ![]() ЃЌ
ЃЌ![]() гы
гы ![]() НЛгкЕу
НЛгкЕу ![]() ЃЎ
ЃЎ
(1) ЧѓжЄЃК![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
(2) Шє ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ ![]() КЭ
КЭ ![]() ЕФГЄЖШЃЎ
ЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
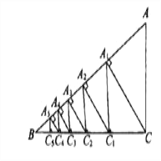
ЁОЬтФПЁПШчЭМЫљЪО,вбжЊ Rt Ёї ACB жа, AC =3, BC =4,Й§жБНЧЖЅЕу C зї CA 1 ЁЭ AB ,ДЙзуЮЊ A 1 ,дйЙ§ A 1 зї A 1 C 1 ЁЭ BC ,ДЙзуЮЊ C 1 ,Ё...,етбљвЛжБзїЯТШЅЕУЕНСЫвЛзщЯпЖЮ CA 1 , A 1 C 1 , C 1 A 2 ,Ё,дђЕк10ЬѕЯпЖЮ A 5 C 5 =________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
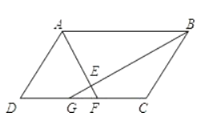
ЁОЬтФПЁПдкЦНааЫФБпаЮABCDжаЃЌЗжБ№вдADЁЂBCЮЊБпЯђФкзїЕШБпЁїADEКЭЕШБпЁїBCFЃЌСЌНгBEЁЂDFЃЎЧѓжЄЃКЫФБпаЮBEDFЪЧЦНааЫФБпаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЖдRtЁїOABвРДЮНјааЮЛЫЦЁЂжсЖдГЦКЭЦНвЦБфЛЛКѓЕУЕНЁїOЁфAЁфBЁфЃЎ
ЃЈ1ЃЉдкзјБъжНЩЯЛГіетМИДЮБфЛЛЯргІЕФЭМаЮЃЛ
ЃЈ2ЃЉЩшP(x,y)ЮЊЁїOABБпЩЯШЮвЛЕуЃЌвРДЮаДГіетМИДЮБфЛЛКѓЕуPЖдгІЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќжБНЧШ§НЧаЮOABЕФШ§ИіЖЈЕуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЙ§AзїyжсЕФДЙЯп
ЃЌЙ§AзїyжсЕФДЙЯп![]() .ЕуCдкxжсЩЯвдУПУы
.ЕуCдкxжсЩЯвдУПУы![]() ЕФЫйЖШДгдЕуГіЗЂЯђгвдЫЖЏЃЌЕуDдк
ЕФЫйЖШДгдЕуГіЗЂЯђгвдЫЖЏЃЌЕуDдк![]() ЩЯвдУПУы
ЩЯвдУПУы![]() ЕФЫйЖШЭЌЪБДгЕуAГіЗЂЯђгвдЫЖЏЃЌЕБЫФБпаЮABCDЮЊЦНааЫФБпаЮЪБCЁЂDЭЌЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
ЕФЫйЖШЭЌЪБДгЕуAГіЗЂЯђгвдЫЖЏЃЌЕБЫФБпаЮABCDЮЊЦНааЫФБпаЮЪБCЁЂDЭЌЪБЭЃжЙдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() .ЕБCЁЂDЭЃжЙдЫЖЏЪБЃЌНЋЁїOABбиyжсЯђгвЗелЕУЕНЁї
.ЕБCЁЂDЭЃжЙдЫЖЏЪБЃЌНЋЁїOABбиyжсЯђгвЗелЕУЕНЁї![]() ЃЌ
ЃЌ![]() гыCDЯрНЛгкЕуEЃЌPЮЊxжсЩЯСэвЛЖЏЕу.
гыCDЯрНЛгкЕуEЃЌPЮЊxжсЩЯСэвЛЖЏЕу.
(1)ЧѓжБЯпABЕФНтЮіЪНЃЌВЂЧѓГіtЕФжЕ.
(2)ЕБPE+PDШЁЕУзюаЁжЕЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
(3)ЩшPЕФдЫЖЏЫйЖШЮЊ1ЃЌШєPДгBЕуГіЗЂЯђгвдЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() ЃЌЧыгУКЌ
ЃЌЧыгУКЌ![]() ЕФДњЪ§ЪНБэЪОЁїPAEЕФУцЛ§.
ЕФДњЪ§ЪНБэЪОЁїPAEЕФУцЛ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБНгЬюД№АИЃК
ЂйЃЈЃ5ЃЉЃЋЃЈЃ5ЃЉЃН______ЃЛЂкЃЈЃ5ЃЉЃЋЃЈЃЋ8ЃЉЃН______ЃЛЂл90![]() ЃЈЃ3ЃЉЃН______ЃЛ
ЃЈЃ3ЃЉЃН______ЃЛ
ЂмЃЈЃ5ЃЉЃЃЈЃ3ЃЉЃН______ЃЛЂнЃ16Ѓ8ЃН_____ЃЛЂо8Ѓ16ЃН______ЃЛ
Ђп![]() ЃН______ЃЛЂр
ЃН______ЃЛЂр![]() ЃН_____ЁЃ
ЃН_____ЁЃ
Ђс ![]() ЃН_____ЃЛЂт
ЃН_____ЃЛЂт![]() ЃН______ЁЃ
ЃН______ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФе§ЗНаЮЭјИёжаНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЁїABCЕФЖЅЕуЖМдкИёЕуЩЯЃЌЧыНтД№ЯТСаЮЪЬтЃК

ЃЈ1ЃЉЂйзїГіЁїABCЯђзѓЦНвЦ4ИіЕЅЮЛГЄЖШКѓЕУЕНЕФЁїA1B1C1ЃЌ ВЂаДГіЕуC1ЕФзјБъЃЛ
ЂкзїГіЁїABCЙигкдЕуOЖдГЦЕФЁїA2B2C2ЃЌ ВЂаДГіЕуC2ЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊЁїABCЙигкжБЯпlЖдГЦЕФЁїA3B3C3ЕФЖЅЕуA3ЕФзјБъЮЊЃЈЃ4ЃЌЃ2ЃЉЃЌЧыжБНгаДГіжБЯпlЕФКЏЪ§НтЮіЪН.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com