
����Ŀ����֪����ͼ����ֱ֪�� AB �ĺ�������ʽΪ y 2x 8 ���� x �ύ�ڵ� A ���� y�ύ�ڵ� B ��
��1���� A �� B ��������ꣻ
��2������ P m, nΪ�߶� AB �ϵ�һ�����㣨�� A ��B ���غϣ����� PE x ���� E �� PF y���ڵ� F ������ EF ���ʣ�
����PEF �����Ϊ S ���� S ���� m �ĺ�����ϵʽ��������� S 3ʱ P ������ꣻ
���Ƿ���ڵ� P ��ʹ EF ��ֵ��С�������ڣ���� EF ����Сֵ���������ڣ���˵�����ɡ�

���𰸡���1��A��4��0����B��0��8������2����![]() �������ڣ�EF����Сֵ=OP=
�������ڣ�EF����Сֵ=OP=![]() .
.
��������
��1�������������ϵ���ص�ֱ����ֵ��
��2�����ɵ���ֱ��AB�ϣ��ҳ�m��n�Ĺ�ϵ�����������ε������ʽ��⼴�ɣ�
�ڴ��ڣ�����֤���ı���OEPF�Ǿ��Σ��ɵ�EF=OP�����ݴ��߶���̿�֪����OP��ABʱ����ʱEF��С��
�⣺��1����x=0����y=8��
��B��0��8����
��y=0����-2x+8=0��
��x=4��
��A��4��0����
��2���١ߵ�P��m��n��Ϊ�߶�AB�ϵ�һ�����㣬
��-2m+8=n��
��A��4��0����
��OA=4��
��0��m��4
��PF=m��PE=-2m+8
��![]() =
=![]() PF��PE=
PF��PE=![]() ��m����-2m+8��=
��m����-2m+8��=![]() ����0��m��4����
����0��m��4����
�ڴ��ڣ���ͼ
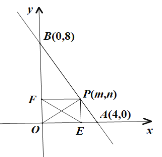
���ɣ���PE��x���ڵ�E��PF��y���ڵ�F��OA��OB��
���ı���OEPF�Ǿ��Σ�
��EF=OP��
��OP��ABʱ����ʱEF��С��
��A��4��0����B��0��8����
��AB=![]()
��S��AOB=![]() ��OA��OB=
��OA��OB=![]() ��AB��OP��
��AB��OP��
![]() ��
��
��EF����Сֵ=OP=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
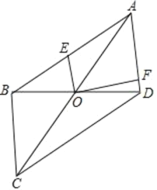
����Ŀ����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB��5��AD��3��E��AB�ϵ�һ�㣬F��AD�ϵ�һ�㣬����BO��FO��
��1������EΪAB�е�ʱ����EO�ij��ȣ�
��2�����߶�AO��ȡֵ��Χ��
��3����EO��FOʱ������EF����֤��BE+DF��EF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
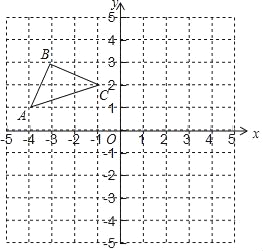
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��֪��ABC������������ֱ�ΪA����4��1����B����3��3����C����1��2����
��1��������ABC����x��ԳƵġ�A1B1C1����A��B��C�ĶԳƵ�ֱ��ǵ�A1��B1��C1��ֱ��д����A1��B1��C1�����꣺A1���� ������ ������B1���� ������ ������C1���� ������ ������
��2��������C����y��ĶԳƵ�C2������C1C2��CC2��C1C����ֱ��д����CC1C2��������� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���EΪAD���е㣬�ӳ�CE��BA���ӳ����ڵ�F��
��1����֤��AB=AF��
��2����BC=2AB����BCD=110�������ABE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�A(a��0)��B(0��b)��C(��a��0)����![]() +b2��4b+4��0
+b2��4b+4��0
(1)��֤����ABC��90����
(2)����ABO��ƽ���߽�x����һ��D����D������ꣻ
(3)��ͼ2��ʾ��A��B������x�ᡢy���ϵ�λ�ò��䣬���߶�AB����������M��N�������MON��45�������н��ۣ���BM+AN��MN����BM2+AN2��MN2����������ֻ��һ�����۳����������ж���һ�����۳�������֤�������Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ��![]() �Ķ�����ڸ���ϣ���
�Ķ�����ڸ���ϣ���![]() ������Ϊ
������Ϊ![]() ��
��

����![]() ����ƽ��5����λ��õ���Ӧ��
����ƽ��5����λ��õ���Ӧ��![]() ������
������![]() �����
����д��![]() �����ꣻ
�����ꣻ
����ԭ��![]() Ϊ�Գ����ģ�����
Ϊ�Գ����ģ�����![]() �����ԭ��
�����ԭ��![]() �ԳƵ�
�ԳƵ�![]() ����д����
����д����![]() �����꣮
�����꣮
����ԭ��OΪ��ת���ģ�������![]() ˳ʱ����ת90����ͼ����A3B3C3����д��C3�����꣮
˳ʱ����ת90����ͼ����A3B3C3����д��C3�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC����A=36����AB�Ĵ�ֱƽ���߽�AC��D�������н��ۣ��١�C=72������BD�ǡ�ABC��ƽ���ߣ��ۡ�ABD�ǵ��������Σ��ܡ�BCD�ǵ��������Σ�������ȷ����____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
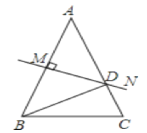
����Ŀ����ͼ����֪��O=30�㣬��B��OM���ϵ�һ�����Դ���ڱ�ON�Ϸ�һƽ�澵������BC��
��ƽ�澵�������������OM�Ľ����ΪE�����OCE�ǵ��������εĸ����У� ��
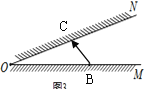
A. 1�� B. 2�� C. 3�� D. 3������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
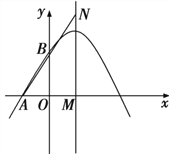
����Ŀ����ͼ��������![]() ��
��![]() ���㣮
���㣮
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() Ϊ�����߶Գ�����x��Ľ��㣬NΪ�Գ�����һ�㣬��
Ϊ�����߶Գ�����x��Ľ��㣬NΪ�Գ�����һ�㣬��![]() ����M��AN�ľ��룮
����M��AN�ľ��룮
![]() �������ߵĶԳ������Ƿ���ڵ�P��ʹ
�������ߵĶԳ������Ƿ���ڵ�P��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д�����������ĵ�
Ϊ���������Σ������ڣ���ֱ��д�����������ĵ�
P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com