
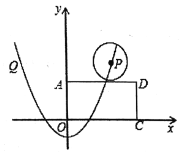
【题目】如图,平面坐标内,矩形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() 的半径为1,当圆心
的半径为1,当圆心![]() 在抛物线上从点
在抛物线上从点![]() 运动到点
运动到点![]() ,则在整个运动过程中,
,则在整个运动过程中,![]() 与矩形
与矩形![]() 只有一个公共点的情况共出现______次.
只有一个公共点的情况共出现______次.
科目:初中数学 来源: 题型:
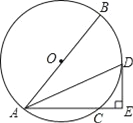
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月6日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车一次共运输土方31吨,5辆大型渣土运输车与6辆小型渣土运输车一次共运输土方70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
(2)该渣土运输公司决定派出大、小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不少于148吨,且小型渣土运输车至少派出2辆,则有哪几种派车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
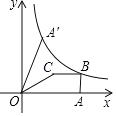
【题目】如图,平面直角坐标系xOy中,四边形OABC的边OA在x轴正半轴上,BC∥x轴,∠OAB=90°,点C(3,2),连接OC.以OC为对称轴将OA翻折到OA′,反比例函数y=![]() 的图象恰好经过点A′、B,则k的值是( )
的图象恰好经过点A′、B,则k的值是( )
A. 9B. ![]() C.
C. ![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
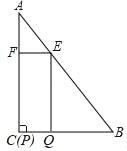
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示:
时间x(天) | 1≤x≤7 | 8≤x≤14 |
售价(元/斤) | 第1次降价后的价格 | 第2次降价后的价格 |
销量(斤) | 80﹣3x | 120﹣x |
储存和损耗费用(元) | 40+3x | 3x2﹣64x+400 |
已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x≤14)之间的函数关系式,并求出第几天时销售利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
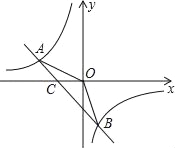
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AB.C内接于⊙0,点D在半径OB的延长线上,∠BCD=∠A=30°.
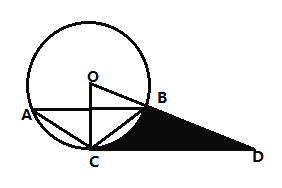
(1)判断直线CD与⊙0的位置关系,并说明理由
(2)若⊙0的半径为1,求阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com