
【题目】如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+![]() )π.
)π.
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+![]() ﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
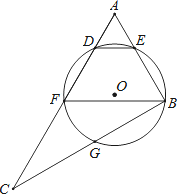
【答案】(1)r=1+![]() ;(2)圆心O在直线BF上.理由见解析.
;(2)圆心O在直线BF上.理由见解析.
【解析】
(1)设⊙O的半径为r,再根据弧长公式即可得出结论;
(2)先根据DE∥BF得出∠ADE=∠AFB,再根据圆内接四边形的性质得出∠AFB+∠DEB=180°,进而得出AF的长.在Rt△ABC中,根据直角三角形的性质求出BF的长,再由B、F都在⊙O上即可得出结论.
(1)设⊙O的半径为r,
∵∠ABC=90°
∴弧EFG所对的圆心角的度数为180°,
∴![]() =(1+
=(1+![]() )π,即r=1+
)π,即r=1+![]() ;
;
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,
∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,
∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,
∴∠AFB=∠AED,
∴∠ADE=∠AED,
∴AD=AE=a.
∵DF=2+![]() ﹣a,
﹣a,
∴AF=AD+DF=2+![]() .
.
在Rt△ABC中,∠ABC=90°且F为AC中点,
∴BF=AF=2+![]() .
.
∵r=1+![]() ,
,
∴BF=2r.
∵B、F都在⊙O上,
∴BF为⊙O直径,
∴点O在直线BF上.


科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
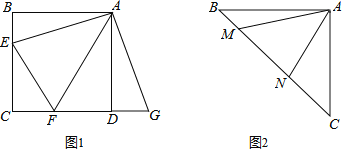
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、P、B、C是⊙O上的四点,∠APC=∠CPB=60°,过点C作CM∥BP交PA的延长线于点M.
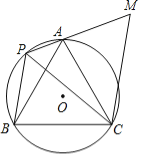
(1)求证:△ACM≌△BCP;
(2)若PA=1,PB=2,求△PCM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,给出下列条件:①
中,给出下列条件:①![]() ②
②![]() ③
③![]() ④
④![]()
其中能判定四边形是平行四边形的组合是________或 ________或_________或_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
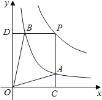
【题目】函数![]() 和
和![]() 在第一象限内的图象如图所示,点
在第一象限内的图象如图所示,点![]() 是
是![]() 的图象上一动点,作
的图象上一动点,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,作
,作![]() 轴于点
轴于点![]() ,交
,交![]() 的图象于点
的图象于点![]() ,给出如下结论:①
,给出如下结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() 与
与![]() 始终相等;③四边形
始终相等;③四边形![]() 的面积大小不会发生变化;④
的面积大小不会发生变化;④![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
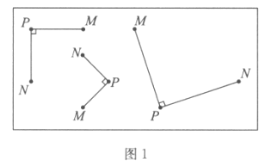
【题目】如图1中的三种情况所示,对于平面内的点M,点N,点P,如果将线段PM绕点P顺时针旋转90°能得到线段PN,就称点N是点M关于点P的“正矩点”.
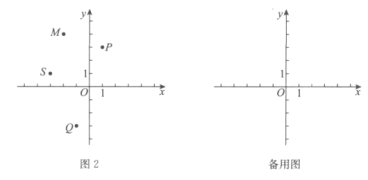
(1)在如图2所示的平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() .
.
①在点P,点Q中,___________是点S关于原点O的“正矩点”;
②在S,P,Q,M这四点中选择合适的三点,使得这三点满足:
点_________是点___________关于点___________的“正矩点”,写出一种情况即可;
(2)在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为
与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为![]() .
.
①当点A在x轴的正半轴上且OA小于3时,求点C的横坐标![]() 的值;
的值;
②若点C的纵坐标![]() 满足
满足![]() ,直接写出相应的k的取值范围.
,直接写出相应的k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com