
分析 (1)取出绿球的概率=1-取出黄球的概率;
(2)设袋中有绿球x个,根据从口袋中取出一个球是黄球的概率是$\frac{2}{5}$列出方程$\frac{18}{x+18}$=$\frac{2}{5}$,求解即可.
解答 解:(1)P(取出绿球)=1-P(取出黄球)=1-$\frac{2}{5}$=$\frac{3}{5}$;
(2)设袋中有绿球x个.
根据题意,得:$\frac{18}{x+18}$=$\frac{2}{5}$,
解得:x=27,
经检验:x=27是所列方程的解.
答:袋中的绿球有27个.
点评 此题考查概率了概率公式.用到的知识点为:概率=所求情况数与总情况数之比;组成整体的各部分的概率之和为1.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4.6×1010元 | B. | 0.46×1011元 | C. | 46×109元 | D. | 4.6×109元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
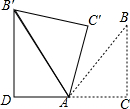 如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
如图,△ABC为等腰直角三角形,∠ACB=90°,将△ABC绕点 A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )| A. | 2 | B. | 3 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com