

分析 (1)连接AI,根据正方形的性质和三角形内角和定理计算即可;
(2)连接AI、BH、BD,证明A、H、C、D四点共圆,得到∠AHC=∠ABC=90°,根据垂直的定义证明即可;
(3)作BK⊥HC于K,连接AI,证明四边形FBKH是正方形,根据直角三角形的性质计算即可.
解答 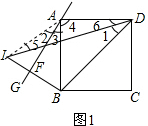 解:(1)如图1,连接AI,
解:(1)如图1,连接AI,
∵四边形ABCD是正方形,
∴∠4=90°,AB=AD.
∵点I与B点关于直线AG对称,∠3=30°,
∴∠2=30°,AI=AB.
∴AI=AD.∴∠5=∠6=(180°-150°)÷2=15°.
又∵∠ADB=45°,
∴∠1=30°.
(2)如图2,分别连接AI、BH、BD,同(1)可证:∠1=∠2,∠3=∠2.
∴∠1=∠3.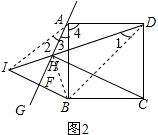
∵点I与B点关于直线AG对称,
∴HI=HB,
∴∠BHD=∠4=90°.
又∵∠BCD=90°,
∴A、H、C都在以BD为直径的圆上.
∴∠AHC=∠ABC=90°.
∴CH⊥AG.
(3)作BK⊥HC于K,连接AI,
由(1)得∠BID=45°.
又∵∠HFI=90°,
∴FH=FI=FB.
由(2)知:∠HFB=90°.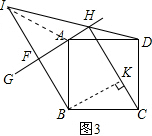
∴四边形FBKH是正方形.
∴HK=FB=BK.
在Rt△AFB中,∵∠BAG=60°,
∴∠ABG=30°.又∵AB=2,
∴AF=1,FB=$\sqrt{3}$AF=$\sqrt{3}$.
同理可得:KC=1.
∴CH=HK+KC=$\sqrt{3}$+1.
点评 本题考查了正方形的性质、轴对称的性质、旋转的性质以及等腰三角形的判定与性质、面积的计算方法;熟练掌握正方形和轴对称的性质得出等腰三角形,进一步得出角之间的关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证:
如图,在△ABC中,AB=AC,延长AB到D,使BD=AB,E为AB的中点,连结CE、CD,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 红星中学七年级(1)班的李老师在上完“几何图形”第一课时后,给班上的同学们留了这样一道思考题:用六根火柴棒,你能组成四个大小一样的三角形吗?若能,叙述你的做法;若不能,请说明理由.
红星中学七年级(1)班的李老师在上完“几何图形”第一课时后,给班上的同学们留了这样一道思考题:用六根火柴棒,你能组成四个大小一样的三角形吗?若能,叙述你的做法;若不能,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com