
 ������ѧ���꼶��1���������ʦ�����ꡰ����ͼ�Ρ���һ��ʱ�����ϵ�ͬѧ����������һ��˼���⣺��������������������ĸ���Сһ���������������ܣ�������������������ܣ���˵�����ɣ�
������ѧ���꼶��1���������ʦ�����ꡰ����ͼ�Ρ���һ��ʱ�����ϵ�ͬѧ����������һ��˼���⣺��������������������ĸ���Сһ���������������ܣ�������������������ܣ���˵�����ɣ����� ���������������������ĸ���Сһ���������Σ���ͼ��ֻ����������
���  �⣺С���Ľ����ȷ��
�⣺С���Ľ����ȷ��
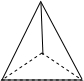
���ɣ���ͼ��ʾ���Ȱ�3������ƴ��һ���ȱ������Σ�������ʣ�µ�3��������ԭ����3��������ϳ�������
������4���棬ÿ���涼��һ����С�������Σ�
���� ������Ҫ������Ӧ����ͼ����ƣ�ͬʱ������ѧ���Ķ��ֲ����������ռ������������õ�ƴ�ɼ��������״�ǽ������Ĺؼ���


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
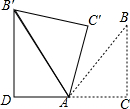 ��ͼ����ABCΪ����ֱ�������Σ���ACB=90�㣬����ABC�Ƶ� A��ʱ����ת75�㣬�õ���AB��C�䣬����B����B��D��CA����CA���ӳ����ڵ�D����AC=6����AD�ij�Ϊ��������
��ͼ����ABCΪ����ֱ�������Σ���ACB=90�㣬����ABC�Ƶ� A��ʱ����ת75�㣬�õ���AB��C�䣬����B����B��D��CA����CA���ӳ����ڵ�D����AC=6����AD�ij�Ϊ��������| A�� | 2 | B�� | 3 | C�� | 2$\sqrt{3}$ | D�� | 3$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
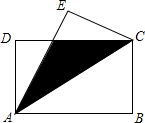 ��ͼ��ABCD�dz����Σ�AB=8��BC=6��������ABC��AC���۹�������B���䵽E����AE��CD��F�����ص����ֵ������
��ͼ��ABCD�dz����Σ�AB=8��BC=6��������ABC��AC���۹�������B���䵽E����AE��CD��F�����ص����ֵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5cm��5cm��12cm | B�� | 3cm��4cm��5cm | C�� | 4cm��6cm��10cm | D�� | 3cm��4cm��8cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7 | B�� | 8 | C�� | 12 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com