练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．函数y=ax2+bx+c与x轴的交点坐标就是方程ax2+bx+c=0的解，若抛物线与x轴无交点，则方程ax2+bx+c=0没有实数解，此时b2-4ac＜0．

    分析 由于抛物线y=ax2+bx+c与x轴的交点坐标就是方程ax2+bx+c=0的解，所以当抛物线与x轴无交点，则方程ax2+bx+c=0无实数解，则根据判别式的意义可得△=b2-4ac＜0．

    解答 解：∵抛物线与x轴无交点，
    ∴方程ax2+bx+c=0没有实数解，
    ∴△=b2-4ac＜0．
    故答案为没有实数解，＜．

    点评 本题考查了抛物线与x轴的交点：对于二次函数y=ax2+bx+c（a，b，c是常数，a≠0），△=b2-4ac决定抛物线与x轴的交点个数：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．在平面直角坐标系xOy中，已知点A、B、C的坐标分别为A（1，0）、B（3，1）、C（3，5），则三角形ABC的面积为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

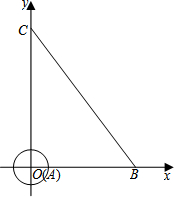    7．如图，在平面直角坐标系中，半径为1的⊙A的圆心与坐标原点O重合，线段BC的端点分别在x轴与y轴上，点B的坐标为（6，0），且sin∠OCB=$\frac{3}{5}$．
    （1）若点Q是线段BC上一点，且点Q的横坐标为m．
    ①求点Q的纵坐标；（用含m的代数式表示）
    ②若点P是⊙A上一动点，求PQ的最小值；
    （2）若点A从原点O出发，以1个单位/秒的速度沿折线OBC运动，到点C运动停止，⊙A随着点A的运动而移动．
    ①点A从O→B的运动的过程中，若⊙A与直线BC相切，求t的值；
    ②在⊙A整个运动过程中，当⊙A与线段BC有两个公共点时，直接写出t满足的条件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知线段AC=12，点D、B在线段AC上．
    （1）若AD=7，DB=2，求BC的长；
    （2）若D为AC的中点，CB=5，求DB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，OP为∠AOB内一条射线，C、D分别为OA、OB上两点，且∠PCO+∠PDO=180°，PC=PD．求证：OP平分∠A0B．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．红星中学七年级（1）班的李老师在上完“几何图形”第一课时后，给班上的同学们留了这样一道思考题：用六根火柴棒，你能组成四个大小一样的三角形吗？若能，叙述你的做法；若不能，请说明理由．
    小明的解答是，不能，因为三根火柴棒只能摆出一个三角形，五根火柴棒可摆出两个三角形（如图所不），六根火柴棒根本不可能摆出四个大小完全相同的三角形．
    你认为小明的解答正确吗？若不正确，试通过画图进行说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．一个多边形的外角和是它的内角和的$\frac{1}{4}$，求这个多边形的边数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列不等式中，是一元一次不等式的有（　　）
    ①3x-7＞0；②2x+y＞3；③2x2-x＞2x2-1；④$\frac{3}{x}$+1＜7．
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．甲、乙两城市间的铁路经过技术改造，列车在甲乙两城市间的运行速度从80千米/时提高到100千米/时，运行时间缩短了3小时．甲、乙两城市间的路程是多少千米？

    查看答案和解析>>

    同步练习册答案