练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】半径为10的⊙O和直线l上一点A，且OA＝10，则直线l与⊙O的位置关系是( )

    A. 相切 B. 相交 C. 相离 D. 相切或相交

    【答案】D

    【解析】分析：根据直线和圆的位置关系来判断.

    详解：设圆心到直线l的距离为d，则d≤10，当d＝10时，d＝r，直线与圆相切；当r＜10时，d＜r，直线与圆相交，所以直线与圆相切或相交.

    故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了提高科技创新意识，我市某中学在“2016年科技节”活动中举行科技比赛，包括“航模”、“机器人”、“环保”、“建模”四个类别（每个学生只能参加一个类别的比赛），各类别参赛人数统计如图：

    请根据以上信息，解答下列问题：

    （1）全体参赛的学生共有 人，“建模”在扇形统计图中的圆心角是 °；

    （2）将条形统计图补充完整；

    （3）在比赛结果中，获得“环保”类一等奖的学生为1名男生和2名女生，获得“建模”类一等奖的学生为1名男生和1名女生，现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动，问选取的两人中恰为1男生1女生的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图（1），若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN，则称这三个正方形为△ABC的外展三叶正方形，其中任意两个正方形为△ABC的外展

    双叶正方形．

    （1）作△ABC的外展双叶正方形ACDE和BCFG，记△ABC，△DCF的面积分别为S1和S2．

    ①如图（2），当∠ACB=90°时，求证：S1=S2；

    ②如图（3），当∠ACB≠90°时，S1与S2是否仍然相等，请说明理由．

    （2）已知△ABC中，AC=3，BC=4，作其外展三叶正方形，记△DCF、△AEN、△BGM的面积和为S，请利用图（1）探究：当∠ACB的度数发生变化时，S的值是否发生变化？若不变，求出S的值；若变化，求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式中不能用平方差公式计算的是（ ）
    A.(x－2y)(2y+x)
    B.(x－2y)(－2y+x)
    C.(x+y)(y－x)
    D.(2x－3y)(3y+2x)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O1与⊙O2的圆心距O1O2＝6cm，且两圆的半径满足一元二次方程x2-6x+8=0，则两圆的位置关系为　( )

    A. 外切 B. 内切 C. 外离 D. 相交

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)完成下面的推理说明:

    已知:如图,∥,、分别平分和.

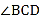
    求证:∥.

    证明:、分别平分和(已知)，

    , ( ).

    ∥( ),

    ( ).

    ( ).

    (等式的性质).

    ∥( ).

    (2)说出(1)的推理中运用了哪两个互逆的真命题.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，□ ABCD中，E是BA延长线上一点，AB＝AE，连结CE交AD于点F，若CF平分∠BCD，AB＝3，则BC的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】不改变分式的值，将分式的分子、分母的各项系数都化为整数，则= ___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠BAC=90°

    （1）先作∠ACB的平分线交AB边于点P，再以点P为圆心，PA长为半径作⊙P；（要求：尺规作图，保留作图痕迹，不写作法）

    （2）请你判断（1）中BC与⊙P的位置关系，并证明你的结论．

    查看答案和解析>>

    同步练习册答案