
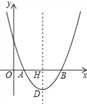
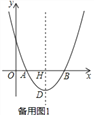
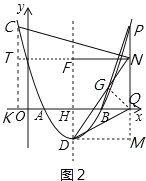
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2��10ax+16a��a��0����x����A��B���㣬�����ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH��
��1����a��ֵ��
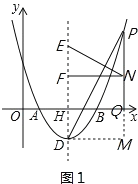
��2����P�ǶԳ����Ҳ��������ϵĵ㣬����PD��PQ��x���ڵ�Q����N���߶�PQ�ϵĵ㣬����N��NF��DH�ڵ�F��NE��PD��ֱ��DH�ڵ�E�����߶�EF�ij���
��3���ڣ�2���������£�����DN��DQ��PB����DN=2QN��NQ��3����2��NDQ+��DNQ=90��ʱ����NC��PB���Գ��������������ڵ�C�����C�����꣮
���𰸡���1��![]() ����2��3����3����C����1��9������
����2��3����3����C����1��9������
�������������������1������y=ax2-10ax+16a������õ�y=0ʱ��x��ֵ���Ӷ�������õ�A��B�����꣬�������ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH���Ӷ��������a��ֵ��
��2��������֪����������Ӧ��ͼ�Σ�Ȼ�����������Ŀ�е�������ϵ��ͨ�������ο������EF�ij���
��3������������Ի�����Ӧ��ͼ�Σ�Ȼ�������Ŀ�еĹ�ϵ���������������ƣ����仯������õ�C�����꣮
�����������1����y=0����x=2��x=8�����A��2��0����B��8��0������AB=6��
��AB=2DH����DH=3��
��OH=2+![]() ����D��5����3�����ੁ3=a��52��10a��5+16a����a=
����D��5����3�����ੁ3=a��52��10a��5+16a����a=![]() ��
��
��2����ͼ1������D��PQ�Ĵ��ߣ���PQ���ӳ����ڵ�M��
��NE��PD�����DPN+��PNE=90�㣬��NF��DE�����FEN+��FNE=90�㣬
�֡�DH��x�ᣬPQ��x�ᣬ��DE��PQ�����FEN=��PNE�����DPM=��ENF�����EFN�ס�DMP��
��![]() �����P��t��
�����P��t�� ![]() ������FN=DM=t��5��PM=
������FN=DM=t��5��PM=![]() +3��������EF=3��
+3��������EF=3��
��3����ͼ2����QG��DN�ڵ�G����DF��PQ�����FDN=��DNQ����2��NDQ+��DNQ=90�㣬
��2��NDQ+��FDN=90�㣬�ߡ�FDM=90�㣬���NDM=2��NDQ�����NDQ=��MDQ����QG=QM=DH=3��
��QN=m����DN=2m����sin��DNM=![]() ��sin��QNG=
��sin��QNG=![]() ��sin��DNM=sin��QNG��
��sin��DNM=sin��QNG��
��![]() ����DM=6=DG����OQ=5+6=11��
����DM=6=DG����OQ=5+6=11��
���P���������ǣ� ![]() =9�����P��11��9����
=9�����P��11��9����
��NG=2m��6����Rt��NGQ��QG2+NG2=QN2��
��32+��2m��6��2=m2���ã�m=3���ᣩ��m=5��
��C��n�� ![]() ������CK��x���ڵ�K����NF��CK�ڵ�K����CT=
������CK��x���ڵ�K����NF��CK�ڵ�K����CT=![]() ��NT=11��n��
��NT=11��n��
��P��11��9������BQ=11��8=3��PQ=9��
��CN��PB��PQ��CK��PQ��x�ᣬ ���CTN�ס�BQP��
��![]() �� ��
�� ��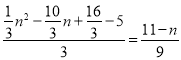 �� ��ã�n=��1��n=10����ȥ����
�� ��ã�n=��1��n=10����ȥ����
���C����1��9����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ�����⣺̽������![]() ��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���
��ͼ�������ʣ�С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽����������С����̽�����̣��벹��������
��ͼ�������ʽ�����̽����������С����̽�����̣��벹��������
��1������![]() ���Ա���x��ȡֵ��Χ�� ��
���Ա���x��ȡֵ��Χ�� ��
��2���±���x��y�ļ����Ӧֵ��
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
| m | ... |
��m��ֵ��
��3����ͼ����ƽ��ֱ������ϵ�У�����������ϱ��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ��

��4����һ��̽�����֣��ú���ͼ���ڵ�һ�����ڵ���͵�������ǣ�1��![]() ������Ϻ�����ͼ��д���ú������������ʣ�д�������ɣ���
������Ϻ�����ͼ��д���ú������������ʣ�д�������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
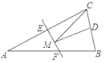
����Ŀ����ͼ������������ABC�ĵױ�BC��Ϊ6�������24����AC�Ĵ�ֱƽ����EF�ֱ�AC��AB����E��F�㣮����DΪBC�ߵ��е㣬��MΪ�߶�EF��һ���㣬����CDM�ܳ�����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��x3x4x5
��2��![]() ��
��
��3������2mn2��2��4mn3��mn+1����
��4��3a2��a3b2��2a����4a����a2b��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��C�ֱ��ڡ�GBE�ı�BG��BE�ϣ���AB=AC��AD��BE����GBE��ƽ������AD���ڵ�D������CD��
��1����֤��CDƽ�֡�ECA��
��2�������BDC���BAC֮���к�������ϵ��������IJ������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������
��1��12+��-3.4��-��-13.4��
��2��![]()
��3��0-5+-25-26
��4��-4��![]() ��
��![]()
��5��![]() ����-24��
����-24��
��6��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Լ����ǵ������һ����Ҫ�����η�ʽ����һ�ż��ڼ�С��һ�����Լ�ȥ��ɽ���棬��ͼ������С���ְּ�ʻ��������һ��ʱ����·��s(ǧ��)��ʱ��t��Сʱ���ĺ�����ϵ������˵������ȷ����( )

A. ������0��1Сʱ���ٶ���60ǧ��/ʱ�� B. ������2��3Сʱ���ٶȱ�0��0.5Сʱ���ٶȿ죻
C. ������0.5Сʱ��1.5Сʱ���ٶ���80ǧ��/ʱ�� D. ������ʻ��ƽ���ٶ�Ϊ60ǧ��/ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����30Ԫ�������з���������Ʒÿ���������y��������ÿ�����ۼ�x��Ԫ���Ĺ�ϵ�������£�
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
��1����֪y��x����һ�κ�����ϵ�������ϱ������y��x֮��Ĺ�ϵʽ.����д���Ա���x��ȡֵ��Χ����
��2������̵�����������Ʒ��ÿ��Ҫ���150Ԫ����ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ��
��3������̵�ÿ������������Ʒ��������Ϊw��Ԫ�������w��x֮��Ĺ�ϵʽ�������ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=BC���Խ���BDƽ��ABC��P��BD��һ�㣬����P��PM^AD��PN^CD������ֱ�ΪM��N��
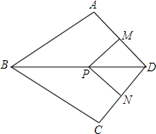
��1����֤��ADB=CDB��
��2����ADC=90������֤���ı���MPND�������Ρ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com