
 如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )
如图,矩形ABDC中,∠BAD的平分线交BC于E.若AB=4,AD=7,则S△DEC=( )| A. | 6 | B. | 7 | C. | 8 | D. | 11 |
分析 由矩形的性质得出∠BAD=∠B=∠C═90°,BC=AD=7,CD=AB=4,证明△ABE是等腰直角三角形,得出BE=AB=4,因此CE=BC-BE=3,S△DEC=$\frac{1}{2}$CE•CD,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠B=∠C═90°,BC=AD=7,CD=AB=4,
∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=4,
∴CE=BC-BE=3,
∴S△DEC=$\frac{1}{2}$CE•CD=$\frac{1}{2}$×3×4=6;
故选:A.
点评 本题考查了矩形的性质、等腰直角三角形的性质、三角形面积的计算;熟练掌握矩形的性质,证明三角形是等腰直角三角形得出CE是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.
已知:如图,有一块面积等于1200cm2的三角形纸片ABC,已知底边与底边BC上的高的和为100cm(底边BC大于底边上的高),要把它加工成一个正方形纸片,使正方形的一边EF在边BC上,顶点D、G分别在边AB、AC上,求加工成的正方形铁片DEFG的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
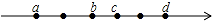 数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示.
数轴上有六个点,每相邻的两个点间的距离都是1个单位长度,有理数a、b、c、d所对应的点是这些点中的4个,位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB∥CD,AB=CD,AC=BD | B. | AD∥BC,AB=CD,∠A=∠B | ||
| C. | AO=BO=CO=DO,AC⊥BD | D. | AO=CO,BO=DO,AB=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )
如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E,在外有一点F,使FA⊥AE,FC⊥BC.在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.有以下结论:①BE=CF;②ME⊥BC;③DE=DN;④图中度数为22.5°的角有5个,其中正确的结论有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3:1 | B. | 9:5 | C. | 5:2 | D. | 4:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com