
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s,过点P作PE∥AC交DC于点E.同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,连接PQ,QE,PQ与AC交与点F,设运动时间为t(s)(0<t<8).
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的
 ;
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.


解:(1)PD=8﹣t,CQ=2t,根据题意得:8﹣t=2t,解得:t=
 ;
;
(2)S四边形PDCQ=
 (PD+CQ)•CD=
(PD+CQ)•CD=
 ×6(8﹣t+2t)=3(8+t)=3t+24,
×6(8﹣t+2t)=3(8+t)=3t+24,
∵PE∥AC,∴
 ,∴
,∴
 =
=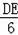
 ,则DE=﹣
,则DE=﹣
 t+6,则EC=6﹣(﹣
t+6,则EC=6﹣(﹣
 t+6)=
t+6)=
 t,
t,
则S△PDE=
 PD•DE=
PD•DE=
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6),S△CQE=
t+6),S△CQE=
 CQ•EC=
CQ•EC=
 ×2t•
×2t•
 t=
t=
 t2,
t2,
则s=3t+24﹣
 (8﹣t)•(﹣
(8﹣t)•(﹣
 t+6)﹣
t+6)﹣
 t2,即s=﹣
t2,即s=﹣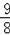
 t2+3t;
t2+3t;
(3)S矩形ABCD=6×8=48,根据由题意得:﹣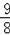
 t2+3t=
t2+3t=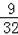
 ×48,解得:t=2或6;
×48,解得:t=2或6;
(4)在直角△PDE中,PD2=(8﹣t)2+(﹣
 t+6)2,
t+6)2,
在直角△COQ中,QE2=(2t)2+(
 t)2,
t)2,
当点E在线段PQ的垂直平分线上时,PD2=QE2,
则(8﹣t)2+(﹣
 t+6)2=(2t)2+(
t+6)2=(2t)2+(
 t)2,
t)2,
解得:t=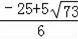
 或
或
 (舍去).则t=
(舍去).则t=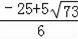
 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
已知△ABC 中, ,
, ,D为BC边延长线上一点,BM平分
,D为BC边延长线上一点,BM平分 ,E
,E 为射线BM上一点.
为射线BM上一点.
(1)如图1,连接CE,
①若CE∥AB,求 的度数;
的度数;
②若CE平分 ,求
,求 的度数.
的度数.
 (2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.
(2)若直线CE垂直于△ABC的一边,请直接写出∠BEC的度数.

25题图1 25题备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

①ac<0;②当x>1时,y的值随x值的增大而减小;③x=2是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<2时,ax2+(b﹣1)x+c>0.上述结论中正确的有 个.( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com