
【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
(1)求点B坐标;
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S;
(3)如图3,在(2)的条件下,点P出发的同时,点Q从O出发,在线段OC上运动,运动速度为每秒2个单位长度,一个点到达终点,另一个点也停止运动.连接PQ,以PQ为一边,在第二象限作等边△PQM,作ME⊥y轴于E,点D为PC中点,作DN⊥BC交y轴于N,若CE=BP,BC=4![]() ,求N的坐标.
,求N的坐标.

【答案】(1)B(﹣6,0);(2)S=3t;(3)N(0,﹣![]() ).
).
【解析】
(1) 由A(2,0),可得OA=2,根据含30°角的直角三角形的性质求出AC 、AB即可解决问题;
(2)如图1,作高线PG,根据直角三角形30度角的性质可得PG的长为t,利用三角形面积公式可得S;
(3)如图2,作辅助线,证明△PCN是等边三角形,再证明△MPC≌△QPN(SAS),得QN=CM,∠MCP=∠QNP=60°,得到30度的直角△MCE,并求得CM=QN=2![]() ,根据CE=BP可得结论.
,根据CE=BP可得结论.
解:(1)∵A(2,0),
∴OA=2,
∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,
∴∠ACO=30°,
∴AC=2OA=4,
∴AB=2AC=8,
∴OB=8﹣2=6,
∴B(﹣6,0).
(2)如图1,过P作PG⊥x轴于G,
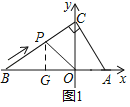
由题意得:BP=2t,
Rt△BPG中,∠B=30°,
∴PG=![]() BP=t,
BP=t,
∴S=![]() =
=![]() ×6×t=3t;
×6×t=3t;
(3)如图2,连接PN、CM.
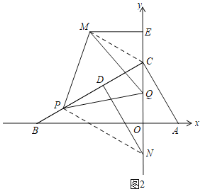
∵BP=2t,BC=4![]() ,
,
∴PC=4![]() ﹣2t,
﹣2t,
∵D是PC的中点,
∴PD=CD,
∵DN⊥PC,
∴PN=CN,
∵∠PCN=60°,
∴△PCN是等边三角形,
∴PC=PN=CN=4![]() ﹣2t,∠NPC=60°,
﹣2t,∠NPC=60°,
∵△PQM是等边三角形,
∴PM=PQ,∠MPQ=60°,
∴∠MPQ=∠CPN=60°,
∴∠MPC=∠QPN,
∴△MPC≌△QPN(SAS),
∴QN=CM,∠MCP=∠QNP=60°,
∵∠PCN=60°,
∴∠MCE=60°,
∵OC=2![]() ,OQ=2t,
,OQ=2t,
∴CQ=2![]() ﹣2t,
﹣2t,
∴QN=CN﹣CQ=4![]() ﹣2t﹣(2
﹣2t﹣(2![]() ﹣2t)=2
﹣2t)=2![]() ,
,
∴CM=QN=2![]() ,
,
Rt△MCE中,∠MCE=60°,
∴CE=![]() CM=
CM=![]() ,
,
∵CE=BP=2t=![]() ,
,
∴ON=QN﹣OQ=2![]() ﹣2t=2
﹣2t=2![]() ﹣
﹣![]() =
=![]() ,
,
∴N(0,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】国庆期间某一位公司老板准备组织员工去上海旅游,甲旅行社承诺:“老板一人免费,员工可享受八折优惠”;乙旅行社承诺:“包括老板在内所有按全票的七五折优惠”,若全票价为2000元
(1)设员工人数为![]() ,甲、乙旅行社收费分别为
,甲、乙旅行社收费分别为![]() 甲(元)和
甲(元)和![]() 乙(元), 分别写出两个旅行社收费的表达式;
乙(元), 分别写出两个旅行社收费的表达式;
(2)当有员工10人时,哪家旅行社更优惠?
(3)当员工人数为多少时,两家旅行社收费相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
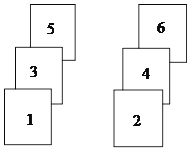
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
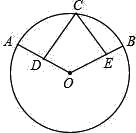
【题目】(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(2)如图:![]() =
=![]() ,D、E分别是半径OA和OB的中点.求证:CD=CE.
,D、E分别是半径OA和OB的中点.求证:CD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每一组数据中的三个数值分别为三角形的三边长:①3,4,5;②6,8,10;③5,12,13;④![]() ,2,
,2,![]() .其中不能构成直角三角形的是____(填序号).
.其中不能构成直角三角形的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com