
【题目】已知:⊙O1与⊙O2相交于A、B两点,且O2在⊙O1上.
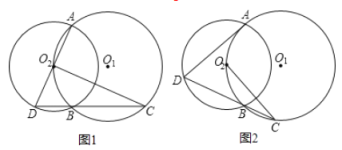
(1)如图1,AD是⊙O2的直径,连DB并延长交⊙O1于点C,求证:CO2⊥AD.
(2)如图2,若AD是⊙O2的非直径的弦,直线DB交⊙O1于点C,则(1)中的结论是否成立,为什么?请加以证明.
【答案】(1)见解析;(2)见解析.
【解析】
(1) 连接AB.根据直径所对的圆周角是直角,得∠ABD=90°;根据等弧所对的圆周角相等,得∠A=∠C,再进一步根据两角对应相等,得△ABD∽△CO2D,从而证明结论;
(2) 连接AO2并延长交圆于E,连接DE、AB.根据直径所对的圆周角是直角,得∠ADE=90°;根据等弧所对的圆周角相等,得∠C=∠1=∠2,从而证明∠ADC+∠C=90°,证明结论.
(1) 连结AB,如图1
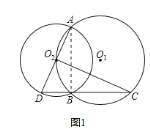
∵AD是⊙O2的直径,
∴∠ABD=90°(直径所对的圆周角是直角),
∴∠BAD+∠BDA=180°-90°=90°(三角形内角和定理),
又∵∠C=∠A(同弧所对圆周角相等),
∴△ABD∽△CO2D,
∴∠ABD=∠CO2D=90°,
即CO2⊥AD.
(2)(1)中的结论仍成立.证明如下:
连接AO2并延长交圆于E,延长CO2交AD于H,连接DE、AB,如图2

∵AE是圆的直径,
∴∠ADE=90°(直径所对的圆周角是直角),
∴∠ADC+∠2=90°,
又∵∠C=∠1=∠2(同弧所对圆周角相等),
∴∠ADC+∠C=90°(等量替换),
∴∠AHD=180°-90°=90°(三角形内角和定理),
则CO2⊥AD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.

(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(﹣![]() ,2),D(
,2),D(![]() ,﹣
,﹣![]() )中,⊙O的“随心点”是_____;
)中,⊙O的“随心点”是_____;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018杭州马拉松竞赛”的个人竞赛项目共有三项:A.“马拉松”,B.“半程马拉松”,C.“迷你马拉松”.小明和小刚参加了该赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为![]() ______.
______.
(2)请用画树状图或列表的方法,求出小明和小刚被分配到同一项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程3x2+3(a+b)x+4ab=0的两个实数根x1、x2满足关系式:x1(x1+1)+x2(x2+1)=(x1+1)(x2+1).判断(a+b)2≤4是否正确,若正确,请加以证明;若不正确,请举一反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】修建隧道可以方便出行.如图:![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要爬坡到山顶
地需要爬坡到山顶![]() 地,再下坡到
地,再下坡到![]() 地.若打通穿山隧道,建成直达
地.若打通穿山隧道,建成直达![]() ,
,![]() 两地的公路,可以缩短从
两地的公路,可以缩短从![]() 地到
地到![]() 地的路程.已知:从
地的路程.已知:从![]() 到
到![]() 坡面的坡度
坡面的坡度![]() ,从
,从![]() 到
到![]() 坡面的坡角
坡面的坡角![]() ,
,![]() 公里.
公里.
(1)求隧道打通后从![]() 到
到![]() 的总路程是多少公里?(结果保留根号)
的总路程是多少公里?(结果保留根号)
(2)求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程约缩短多少公里?(结果精确到0.01)(
地的路程约缩短多少公里?(结果精确到0.01)(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A'B'C,M是BC的中点,P是A'B'的中点,连接PM.若BC=2,∠BAC=30°,则线段PM的最大值是( )
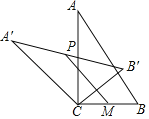
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1;2,△OAC与△CBD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1;2,△OAC与△CBD的面积之和为![]() ,则k的值为( )
,则k的值为( )
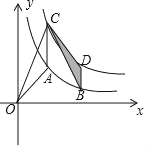
A.2B.3C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学一次趣味运动会50米托盘乒乓球接力项目中(即乒乓球放入托盘内,参赛队员用手托住托盘运送乒乓球),初一(1)班和初一(2)班同台竞技,某时刻,1班的小敏和2班的小文分别位于50米赛道的起点![]() 地和终点
地和终点![]() 地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在
地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在![]() 地(
地(![]() 、
、![]() 、
、![]() 在同一直线上且乒乓球落在
在同一直线上且乒乓球落在![]() 地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往
地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往![]() 地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离
地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离![]() (米)与小敏出发的时间
(米)与小敏出发的时间![]() (秒)之间的函数图象,则当小敏到达
(秒)之间的函数图象,则当小敏到达![]() 地时,小文离
地时,小文离![]() 地还有________米.
地还有________米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com