
����Ŀ����ͼ����![]() �У���D���߶�
�У���D���߶�![]() �ϵĶ��㣬���߶�
�ϵĶ��㣬���߶�![]() �Ƶ�D��ʱ����ת90���õ��߶�
�Ƶ�D��ʱ����ת90���õ��߶�![]() ������
������![]() ������֪
������֪![]() ����B��D�����ľ���Ϊ
����B��D�����ľ���Ϊ![]() ��A��D�����ľ���Ϊ
��A��D�����ľ���Ϊ![]() ��B��E�����ľ���Ϊ
��B��E�����ľ���Ϊ![]() ��
��
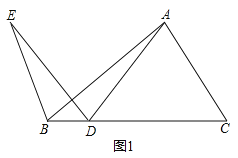
С������ѧϰ�����ľ��飬�ֱ�Ժ���![]() ��
��![]() ���Ա���x�ı仯���仯�Ĺ��ɽ�����̽��
���Ա���x�ı仯���仯�Ĺ��ɽ�����̽��
������С����̽�����̣��벹ȫ������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���![]() ��
��![]() ��x�ļ����Ӧֵ�����±�����˵������ȫ����ʱ�����ֵ����һλС����
��x�ļ����Ӧֵ�����±�����˵������ȫ����ʱ�����ֵ����һλС����
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
| a | 5.66 | 4.32 | b | 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
��2����ͬһƽ��ֱ������ϵ![]() �У������ȫ��ı��и�����ֵ����Ӧ�ĵ�
�У������ȫ��ı��и�����ֵ����Ӧ�ĵ�![]() ��
��![]() ������������
������������![]() ��
��![]() ��ͼ��
��ͼ��
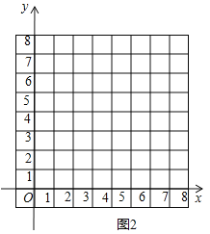
��3����Ϻ���ͼ������⣺
�ٵ�E���߶�![]() ��ʱ��
��ʱ��![]() �ij���ԼΪ___________cm��
�ij���ԼΪ___________cm��
�ڵ�![]() Ϊ����������ʱ��
Ϊ����������ʱ��![]() �ij���xԼΪ___________cm��
�ij���xԼΪ___________cm��
���𰸡���1��![]() ����2��ͼ����������3����6,��3��4.1��7.5.
����2��ͼ����������3����6,��3��4.1��7.5.
��������
��1����![]() ʱ��
ʱ��![]() ��������⣻
��������⣻
��2����㼴�ɣ�
��3���ٵ�E���߶�BC��ʱ������![]() ��������BD���ȣ��ڷ�BE=DE��BE=BD��DE=BE����������ֱ���⼴�ɣ�
��������BD���ȣ��ڷ�BE=DE��BE=BD��DE=BE����������ֱ���⼴�ɣ�
��1����![]() ʱ����B���D�غϣ���ʱ
ʱ����B���D�غϣ���ʱ![]() cm����
cm����![]() ʱ��������
ʱ��������![]() cm��
cm��
��2����㷨�õ�����ͼ����ͼ��ʾ��
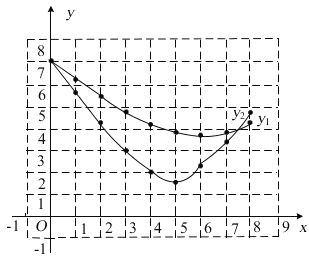
��3�� �ٵ�E���߶�BC��ʱ����![]() �����ݱ��������ݿ�֪����
�����ݱ��������ݿ�֪����![]() ʱ��
ʱ��![]() ,
,![]() cm��
cm��
�ڵ�BE=DEʱ����![]() ����ʱ
����ʱ![]() ��
��![]() ��
��![]() ʱ�����������Σ�
ʱ�����������Σ�![]() ����ȥ����
����ȥ����
��BE=BDʱ����![]() ʱ����ͼ�ϻ���ֱ��
ʱ����ͼ�ϻ���ֱ��![]() ����ͼ��ʾ��
����ͼ��ʾ��
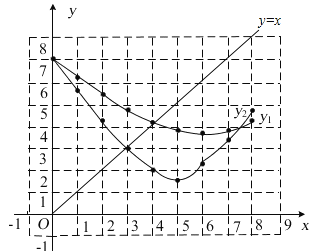
�۲�ͼ���֪����ʱ![]() cm��
cm��
��DE=BEʱ����![]() ʱ���۲�ͼ���֪����ʱ
ʱ���۲�ͼ���֪����ʱ![]() cm��
cm��
�ʴ�Ϊ3��4.1��7.5��


 �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���![]() �У���
�У���![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ����
����![]() �ı�
�ı�![]() �ϵĸ�Ϊ
�ϵĸ�Ϊ![]() ��
��![]() �ı�
�ı�![]() �ϵĸ�Ϊ
�ϵĸ�Ϊ![]() ��
��
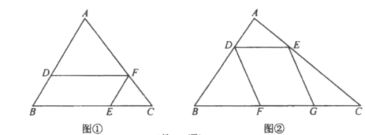
��1����![]() ��
��![]() ������ֱ�Ϊ3��1����
������ֱ�Ϊ3��1����![]() ��
��
��2����![]() ��
��![]() ���ı���
���ı���![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����֤��
����֤��![]() ��
��
��3����ͼ�ڣ���![]() �У���
�У���![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ���
�ϣ���![]() ��
�� ![]() �� ��
�� �� ��
��![]() ��
��![]() ������ֱ�Ϊ3�� 7�� 5����
������ֱ�Ϊ3�� 7�� 5����![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90o��BE�����Ľ�ƽ���ߣ�D��AB���ϣ���DBΪֱ���İ�ԲO������E��
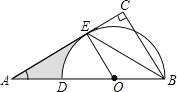
��1����˵����AC��ԲO�����ߣ�
��2������A=30o��ԲO�İ뾶Ϊ4����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����BCΪֱ���ġ�O����CFB�ı�CF�ڵ�A��BMƽ�֡�ABC��AC�ڵ�M��AD��BC�ڵ�D��AD��BM�ڵ�N��ME��BC�ڵ�E��AB2=AF��AC��cos��ABD=![]() ��AD=12��
��AD=12��
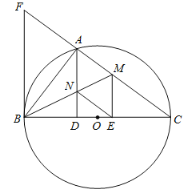
��1����֤����ABF�ס�ACB��
��2����֤��FB�ǡ�O�����ߣ�
��3��֤���ı���AMEN�����Σ���������ε����S��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����A����3��0����B����2��3����C��0��3�����䶥��ΪD��
����A����3��0����B����2��3����C��0��3�����䶥��ΪD��
��1���������ߵĽ���ʽ��
��2�����M��1��m������MB+MD��ֵ��Сʱ����m��ֵ��
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ��
��4���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�N��EΪֱ��AC������һ�㣬����E��EF��ND���������ڵ�F����N��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�λ����Ϊ1��ƽ��ֱ������ϵ�У��������ɰ뾶Ϊ2�ף�Բ�Ľ�Ϊ![]() ��
��![]() ��θ��Ʋ���β���Ӷ��ɣ�����һ��P��A(AΪ����ԭ��)��������ÿ��
��θ��Ʋ���β���Ӷ��ɣ�����һ��P��A(AΪ����ԭ��)��������ÿ��![]() ���ٶ������������˶������ڵ�2019��ʱ��P��������Ϊ( )
���ٶ������������˶������ڵ�2019��ʱ��P��������Ϊ( )
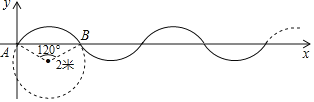
A. ��2B. ��1C. 0D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ��ֱ�x�ᡢy����C��D���㣬������������
��ͼ��ֱ�x�ᡢy����C��D���㣬������������![]() ͼ����A��
ͼ����A��![]() ��4����B��3��m������.
��4����B��3��m������.
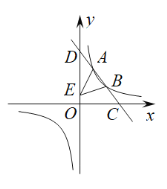
(1)��ֱ��CD�ı���ʽ��
(2)��E���߶�OD��һ�㣬��![]() ����E������ꣻ
����E������ꣻ
(3)�������ͼ��ֱ��д������ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2��3ax��4a��a��0����ͼ����x�ύ��A��B���㣨A��B����ࣩ����y�������ύ�ڵ�C������BC�����κ����ĶԳ�����x��Ľ���ΪE��
��1�������ߵĶԳ�����x��Ľ���E����Ϊ_____����A������Ϊ_____��
��2������EΪԲ�ĵ�Բ��y���ֱ��BC�����У�����������ߵĽ���ʽ��
��3���ڣ�2���������£���ͼ��Q��m��0����x����������һ�㣬����Q��y���ƽ���ߣ���ֱ��BC���ڵ�M���������߽��ڵ�N������CN������CMN��CN���ۣ�M�Ķ�Ӧ��ΪM������ͼ����̽�����Ƿ���ڵ�Q��ʹ��M��ǡ������y���ϣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧС�鵽����Ӣ�ۼ��վ��ִ�ڣ����ڻ��ʵ�ز����˼���ĸ߶ȣ��������£���ͼ�������ڲ�����A���ø�Ϊ1.5m�IJ����AC�������Ӣ�ۼ��MN�M������Ϊ37�㣬Ȼ���ڲ�����B����ͬ���IJ����BD�������Ӣ�ۼ��MN����M������Ϊ45�㣬��������A��B�����ľ���Ϊ15m������N��B��A������һ��ֱ���ϣ�����CD���ӳ���MN�ڵ�E�������������ǵIJ����������������Ӣ�ۼ��MN�ĸ߶ȣ����ο����ݣ�sin37���0.60��cos37���0.80��tan35���0.75��
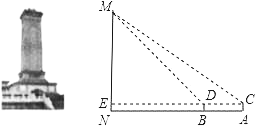
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com