
 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
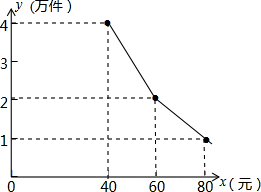 为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为扶持大学生自主创业,市政府提供了80万元无息贷款,用于大学生开办公司,生产并销售自主研发的一种电子产品,并约定用该公司经营的利润偿逐步还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为2500元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将一个大三角形沿虚线剪开分成一个梯形及一个小三角形,若梯形上、下底的长分别是7,14,两腰长为12,16,则剪出的小三角形的周长为( )
如图,将一个大三角形沿虚线剪开分成一个梯形及一个小三角形,若梯形上、下底的长分别是7,14,两腰长为12,16,则剪出的小三角形的周长为( )| A、23 | B、28 | C、31 | D、35 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.
如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
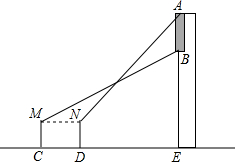 如图,小明在广场上的C处用测角仪正面测量一座楼房墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为30°,然后他正对大楼方向前进10米到达D处,又测得该屏幕上端A处的仰角为45°,已知该楼高18.7米,测角仪MC、ND的高度为1.7米,求广告屏幕AB的长.
如图,小明在广场上的C处用测角仪正面测量一座楼房墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为30°,然后他正对大楼方向前进10米到达D处,又测得该屏幕上端A处的仰角为45°,已知该楼高18.7米,测角仪MC、ND的高度为1.7米,求广告屏幕AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:
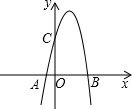 如图,已知二次函数的图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.
如图,已知二次函数的图象过A、C、B三点,点A的坐标为(-1,0),点B的坐标为(4,0),点C在y轴正半轴上,且AB=OC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com