
【题目】已A为顶点的等腰△ABC中,∠ABC、∠ACB的平分线相交于点D,过点D作EF∥BC分别交AB、AC于E、F.
(1)求证:BE=DE;
(2)若△ABC的周长比△AEF的周长大10,试求出BC的长度.

【答案】(1)详见解析;(2)10.
【解析】
(1)由等腰三角形的性质得到∠ABC=∠ACB,根指平行线的性质得到∠AEF=∠ABC,由外角性质即可得到结论
(2)根据等腰三角形的性质和三角形的周长的计算公式即可解题。
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵EF∥BC,
∴∠AEF=∠ABC,∠EDB=∠DBC,
∵∠ABC和∠ACB的平分线交于点D,
∴∠EBD=∠DBC,
又∵∠AEF=∠EBD+∠BDE
∴∠EBD=∠BDE
∴BE=DE;
(2)由(1)证得BE=DE,
同理DF=CF,
∴△AEF的周长=AB+AC,
∵△ABC的周长比△AEF的周长大10,
∴BC=AB+AC+BC-AB-AC=10.


科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过原点的抛物线y=﹣x2﹣2mx(m>1)与x轴的另一个交点为A.过点P(﹣1,m)作直线PD⊥x轴于点D,交抛物线于点B,BC∥x轴交抛物线于点C.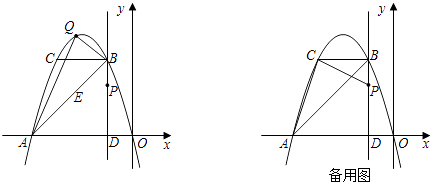
(1)当m=2时.
①求线段BC的长及直线AB所对应的函数关系式;
②若动点Q在直线AB上方的抛物线上运动,求点Q在何处时,△QAB的面积最大?
③若点F在坐标轴上,且PF=PC,请直接写出符合条件的点F在坐标;
(2)当m>1时,连接CA、CP,问m为何值时,CA⊥CP?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 (百分制) | 面试 | 86 | 92 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,并分别赋予它们![]() 和
和![]() 的权.根据四人各自的平均成绩,公司将录取( )
的权.根据四人各自的平均成绩,公司将录取( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方与同学一起去郊游,看到一棵大树斜靠在一小土坡上,他想知道树有多长,于是他借来测角仪和卷尺.如图,他在点C处测得树AB顶端A的仰角为30°,沿着CB方向向大树行进10米到达点D,测得树AB顶端A的仰角为45°,又测得树AB倾斜角∠1=75°.
(1)求AD的长.
(2)求树长AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点P从点C开始,按
,若动点P从点C开始,按![]() 的路径运动,且速度为每秒1cm,设出发的时间为t秒.
的路径运动,且速度为每秒1cm,设出发的时间为t秒.

![]() 出发2秒后,求
出发2秒后,求![]() 的面积;
的面积;
![]() 当t为几秒时,BP平分
当t为几秒时,BP平分![]() ;
;
![]() 问t为何值时,
问t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问

(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1,L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com