
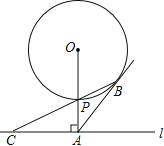
【题目】如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)求证:AB=AC;
(2)若PC=2![]() ,求⊙O的半径及PB的长..
,求⊙O的半径及PB的长..
【答案】(1)证明见解析;(2)⊙O的半径为3,线段PB的长为![]() .
.
【解析】
试题分析:(1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC推出52-r2=(2![]() )2-(5-r)2,求出r,证△DPB∽△CPA,得出
)2-(5-r)2,求出r,证△DPB∽△CPA,得出![]() ,代入求出即可.
,代入求出即可.
试题解析:(1)如图1,连接OB.
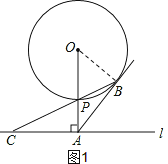
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)如图2,延长AP交⊙O于D,连接BD,
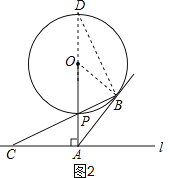
设圆半径为r,则OP=OB=r,PA=5-r,
则AB2=OA2-OB2=52-r2,
AC2=PC2-PA2=(2![]() )2-(5-r)2,
)2-(5-r)2,
∴52-r2=(2![]() )2-(5-r)2,
)2-(5-r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴![]() ,
,
∴![]() ,
,
解得:PB=![]() .
.
∴⊙O的半径为3,线段PB的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 有一个角为60°的三角形是等边三角形
B. 底边相等的两个等腰三角形全等
C. 有一个角是40°,腰相等的两个等腰三角形全等
D. 两直线平行,内错角相等的逆命题是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx﹣3且y随x的增大而增大,那么它的图象经过( )
A. 第二、三、四象限B. 第一、二、三象限
C. 第一、三、四象限D. 第一、二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】掷一枚质地均匀的硬币10次,下列说法正确的是( )
A. 可能有5次正面朝上 B. 必有5次正面朝上
C. 掷2次必有1次正面朝上 D. 不可能10次正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
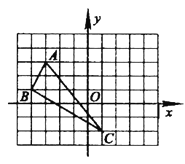
【题目】在平面直角坐标系中, 三角形ABC三个顶点的位置如图(每个小正方形的边长均为1).把三角形ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后得到三角形A′B′C′(其中A′、B′、C′分别是A、B、C的对应点.)
(1)直接写出A′、B′、C′三点的坐标:A′(____,____);B′(____,____);C′(____,____).
(2)求三角形ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com