
Àƒäãá¢À¢á°§´ø±¿¨ùƒ¥æÀÂØØꧡ—¿Ê°äÑÆë´¿»¿¨¢ˆíÅÝõ£þçûá°¡áåš¿Ê°äüŸá¢ÈÛØîøˆ¥æÑÆçËÑâëõ°èíãüŸ¿Ê°äçáòÝ¥ðòúØØÑÆçËÑâëõ°èíãüŸ¿Ê°äòÝ¥ðçá![]() ÝÑȘÆèÆÖØØÑÆ£¿ÆÅóðù«àööþȘüàÆè¥æÑÆçËÑâæ—55䚤µÈ˜åìÆè¥æÀÂØØê§ÑƤüæ—20äšÈ˜ëõ°èêù¡ûüŸ¡áåš¿Ê°äàööþÈÛ
ÝÑȘÆèÆÖØØÑÆ£¿ÆÅóðù«àööþȘüàÆè¥æÑÆçËÑâæ—55䚤µÈ˜åìÆè¥æÀÂØØê§ÑƤüæ—20äšÈ˜ëõ°èêù¡ûüŸ¡áåš¿Ê°äàööþÈÛ
È´ÂþÈˋúŠ¡ªƒïäãØãúµ¥æÀÂØØê§ÑÆçËÑâëõ°è¡áåš¿Ê°äàööþ¡¼ÅÒÑÁèìäšÈ£
ȴ·ÈˋíãüŸ¡áåš¿Ê°ä¿ýëÑæò200ë·åˆÈ˜àÓ¿«¯Çëõ°èçá¿Ê°äꢡѢŸÈ˜áúûÇ¥æÀÂØØê§ÑÆ¢è£þ¿Ê°ä¢Ÿ¡¼ÑÁèìë·åˆÈ¢
ÀƒÇÞ¯¡À¢È´1Èˋ¥æÑÆçËÑâëõ°è¡áåš¿Ê°äàööþÅÒ100äšÈ˜ØØÑÆçËÑâëõ°è¡áåš¿Ê°äàööþÅÒ80äšÈ£È´2Èˋ¥æÑÆ¢è£þ¿Ê°ä¢Ÿ150ë·È˜ØØÑÆ¢è£þ¿Ê°ä¢Ÿ50ë·ÈÛ
Àƒ§ãö—À¢
(1)¯î¿Ê°äæÉꢢÇæ¼çËö£1ȘáúûÇÆÅ¥æçËÑâæ—çá¿Ê°äê¢+¥æØؤüæ¼çá¿Ê°äê¢=1Șà¶èÒØØÑÆçËÑâëõ°èÅÒ؈xäšÈ˜å·¥æçËÑâëõ°èÅÒ؈1.25xäšÈ˜¡ªƒïçàꢿÄüçò§êÅñøò§ñ§°äýÂúµ§ã¥Ç¢è.
(2)üà¥óùÐØØÑÆëõ°èçá¿Ê°äê¢È˜¡ªƒïùªí¥Ýà⻥Ǣèçû°—ØØÑÆ¢è£þçûçá¿Ê°ä¢ŸÈ˜¥äѽçû°—¥æ£þçûçá¿Ê°ä¢Ÿ.
§ãȤȴÂþÈˋèÒ¥æÀÂØØê§ÑÆçËÑâëõ°è¡áåš¿Ê°äàööþ¡¼ÅÒ1.25xäšÈ˜xäš
ØâäãØãçûȤ![]()
í«âÚçûȤ![]()
§ãçûȤ xȧ80ÈÛ
ƒÙ¥šîÕȤxȧ80òúåÙñ§°äçá§ãÈÛ
ÀÁ1.25x=100(äš)
ÇÞȤ¥æÑÆçËÑâëõ°è¡áåš¿Ê°äàööþÅÒ100äšÈ˜ØØÑÆçËÑâëõ°è¡áåš¿Ê°äàööþÅÒ80äšÈ£
ȴ·ÈˋØØÑÆëõ°èçá¿Ê°äê¢![]()
ØØÑÆ¢è£þ¿Ê°ä¢ŸÈ¤![]() ȧ50È´ë·ÈˋÈÛ
ȧ50È´ë·ÈˋÈÛ
¥æÑÆ¢è£þ¿Ê°ä¢ŸÈ¤200-50=150È´ë·ÈˋÈÛ
ÇÞȤ¥æÑÆ¢è£þ¿Ê°ä¢Ÿ150ë·È˜ØØÑÆ¢è£þ¿Ê°ä¢Ÿ50ë·ÈÛ


 à¨áÉýã¢Äأ݃¤ûƒÚüçêÅÇÞ¯¡
à¨áÉýã¢Äأ݃¤ûƒÚüçêÅÇÞ¯¡
| áõ¥Ñ | ¡ÔøÅ¢ö°ä | áõ¥Ñ | °¾øÅ¢ö°ä |
| ¡ÔØ£ | ¡ÔØ£ûãñî¢ö°äëó¥—ÈÀ | °¾Ø£ | °¾Ø£ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôѱ | ¡Ôѱûãñî¢ö°äëó¥—ÈÀ | °¾Ñ± | °¾Ñ±ûãñî¢ö°äëó¥—ÈÀ |
| ¡Ôà» | ¡Ôà»ûãñî¢ö°äëó¥—ÈÀ | °¾à» | °¾à»ûãñî¢ö°äëó¥—ÈÀ |
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢§þáõÀ¯öÍØ£ÀݧÖȘÅÀû¼ëã°—éâè§È˜ù«ÇÆ觧ééâç§è§ÑËçá¿»°äøÅȘøÅëƒÅïüÂêùØ£ÑöòÝ¥ðÈÛèÒù«ÇÆ觧鰗ñ¤µùªÆûçáòÝ¥ðöˆtÈ´ñøøÆÈˋȘùªæÔçáôñ°äöˆsÈ´ûæÈˋȘsÆŠtøÛ¥ðçá¤₤ò»¿ÄüçàÓë¥ùªòƒÈ˜üôêÅùçñ´ÇÚöµçáòúÈ´ Èˋ

AÈÛÅÀû¼øÅëƒÅïüÂÆûêù20ñøøÆ
BÈÛÅÀû¼ÅïüÂú¯éâè§çá󧃪ùìÑàöˆû¢ñøøÆ70ûæ
CÈÛÅÀû¼åÖèüò—¿»°äøÅùªæÔçáôñ°äöˆ6600ûæ
DÈÛÅÀû¼ÅïüÂú¯éâè§çá󧃪ùìÑàǵÆÖÅïü¤µéâè§çá󧃪ùìÑà
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜![]() øÅȘ
øÅȘ![]() Ș
Ș![]() ÈÛ
ÈÛ![]() ÀÂ
ÀÂ![]() òúÝÔ
òúÝÔ![]() ÀÂ
ÀÂ![]() ÝÔèüçáÑ₤çÐȘ
ÝÔèüçáÑ₤çÐȘ![]() ÇÆ
ÇÆ![]() °—ñÂü·
°—ñÂü·![]() åùÑ₤Șë˜òÝ
åùÑ₤Șë˜òÝ![]() ØåüÁë˜çáùìÑàÇÆ
ØåüÁë˜çáùìÑàÇÆ![]() °—ñÂü·
°—ñÂü·![]() åùÑ₤Ș
åùÑ₤Ș![]() åùÑ₤ç§
åùÑ₤ç§![]() ëÈø¿ÈÛ
ëÈø¿ÈÛ![]() öˆ
öˆ![]() øÅçÐÈÛ
øÅçÐÈÛ
![]() òå䧃¢
òå䧃¢![]() çáÅöæÇȘýÂùçû¼âÚÆèÈÛ
çáÅöæÇȘýÂùçû¼âÚÆèÈÛ
![]() åÖåùÑ₤¿»°äøÅȘùáÝÔÅö
åÖåùÑ₤¿»°äøÅȘùáÝÔÅö![]() ¢èáÉ°èöˆí»ñ§ÅöôÞÈ¢àÓáÉúµí»ñ§ÅöçáÝÔ°ÊÈÛ
¢èáÉ°èöˆí»ñ§ÅöôÞÈ¢àÓáÉúµí»ñ§ÅöçáÝÔ°ÊÈÛ
![]() çÝ
çÝ![]() öˆÑÁèìòÝȘ
öˆÑÁèìòÝȘ![]() çáûÌ£»æŸÇµÈ¢æŸÇµûÌ£»òúÑÁèìÈ¢
çáûÌ£»æŸÇµÈ¢æŸÇµûÌ£»òúÑÁèìÈ¢

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢èŸÜÖòÅá°îÏÅÈ°Õîªç¼ýÕȘAâÁîÏèºóÿ¿ýüÚçË°çȘBâÁîÏèºæ½¿¨§£°çÀÂù§¥Ø°ççàȘCâÁîÏèºý§ÅÅȘDâÁîÏèºÈ´óðù■ÈˋȘ¡ªƒïç¼ýէÿ«£Ìøóêùý£ëõí«çáë°¥óë¥ÈÛ
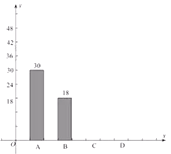
âÁÅë | óçò» | óçôò |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
È´1ÈˋîÏ躿ý________àùȘ ![]() ________Ș
________Ș ![]() ________ȣ
________È£
È´2Èˋý¿à¨ä¾Åöë°¥óë¥È£
È´3ÈˋඡûÅÈ¿ýÆÅ2000àùȘóÿ¿ýüÚçË°ççáÆÅ________àùÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥1ȘåÖó§ûÌøݧúæ½ÝõüçøÅȘأÇö¤₤ò»y=ˋ2x+8çáë¥üµÆŠxøÃȘyøÃñøÝÞ§£ÆÖçÐAȘçÐCȘ¿»çÐAæ¼ABÀëxøÃȘǿæÐöˆçÐAȘ¿»çÐCæ¼CBÀëyøÃȘǿæÐöˆçÐCȘê§ä¾Ç¿üÔüÁ§£ÆÖçÐBÈÛ

È´1ÈˋüÔÑöABȘBCȘACçá°ÊñøÝÞöˆAB=ÀÀ ÀÀȘBC=ÀÀ ÀÀȘAC=ÀÀ ÀÀÈ£
È´2ÈˋíÜç±ë¥1øÅçáÀ¼ABCȘò¿çÐAÆŠçÐCøĤüȘå짨íÜ籤µçáë¥Åöí¿¢ˆÈ˜íܤÜDE§£ABÆÖçÐDȘ§£ACÆÖçÐEȘ꘧ÆCDȘàÓë¥2ÈÛ
úŠÇÆüôêÅAÀÂBê§äãøÅàöîÀØ£äãæ¼ÇÞȘöØîÀåþÀÀ ÀÀäãÈÛ
AȤÂìúµüÔÑöADçá°ÊÈ£
ÂÖåÖyøÃèüȘòúñþÇÌåÖçÐPȘò¿çûÀ¼APDöˆçàî■໧úÅöÈ¢à¶ÇÌåÖȘúŠøݧÆÅÇ°—ñ«¤üä¾¥±çáùªÆÅçÐPçáæ½ÝõÈ£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ
BȤÂìúµüÔÑöDEçá°ÊÈ£
ÂÖåÖæ½Ýõó§ûÌáÖȘòúñþÇÌåÖçÐPÈ´°»çÐBëãÈˋȘò¿çûØåçÐAȘPȘCöˆÑËçÐçá໧úÅöÆŠÀ¼ABCà¨çàÈ¢à¶ÇÌåÖȘúŠøݧÆÅÇ°—ùªÆÅñ«¤üä¾¥±çáçÐPçáæ½ÝõÈ£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢À¼![]() åÖó§ûÌøݧúæ½ÝõüçøÅçáö£øûàÓë¥ùªòƒ.
åÖó§ûÌøݧúæ½ÝõüçøÅçáö£øûàÓë¥ùªòƒ.
È´1Èˋæ¼°—À¼![]() ¿ÄÆÖ
¿ÄÆÖ![]() øÃÑå°óçáÀ¼
øÃÑå°óçáÀ¼![]() ȘýÂÅÇ°—À¼
ȘýÂÅÇ°—À¼![]() ¡¼ÑËçÐçáæ½ÝõÈ£
¡¼ÑËçÐçáæ½ÝõÈ£
È´2Èˋ§¨À¼![]() ü·ÆØó§Øó6¡—çËö£È˜æ¼°—ó§Øó¤µçáÀ¼
ü·ÆØó§Øó6¡—çËö£È˜æ¼°—ó§Øó¤µçáÀ¼![]() ȘýÂÅÇ°—À¼
ȘýÂÅÇ°—À¼![]() ¡¼ÑËçÐçáæ½ÝõÈ£
¡¼ÑËçÐçáæ½ÝõÈ£
È´3Èˋ¿ÜýšÀ¼![]() ¤ëÀ¼
¤ëÀ¼![]() Șù■ûúòúñþ¿ÄÆÖá°øÝüÔÑå°óÈ¢à¶òúȘúŠÆûÇøüÔä¾£Ù°—Ñå°óøÃÈÛ
Șù■ûúòúñþ¿ÄÆÖá°øÝüÔÑå°óÈ¢à¶òúȘúŠÆûÇøüÔä¾£Ù°—Ñå°óøÃÈÛ
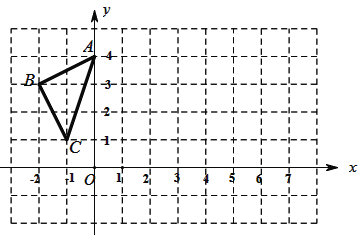
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢RtÀ¼ABCøÅȘÀüACB=90ÀÐȘAC=BCȘçÐDåÖÅÝÝÔABèüȘúØAD=ACȘ¿»çÐBæ¼BEÀëCD§£CDçáîÆ°ÊüÔÆÖçÐEÈÛ
È´1Èˋ£Ù°—ñ«¤üäãØãçáë¥ÅöÈ£
È´2ÈˋúµÀüBCDçáÑàò»È£
È´3ÈˋúµøÊȤCD=2BEÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥ùªòƒÈ˜åÖó§ûÌøݧúæ½ÝõüçøÅȘOöˆæ½ÝõåÙçÐȘøÝüÔyȧkx+bƒÙ¿»çÐAÈ´ˋ2Șˋ1ÈˋȘ§£yø᤯ŠøÃÆÖçÐBȘúØÀüABOȧ30ÀÐȘ¿»çÐAæ¼øÝüÔACÀëxøÃÆÖçÐCȘçÐPåÖøÝüÔACèüÈÛ

È´1ÈˋkȧÀÀ ÀÀÈ£bȧÀÀ ÀÀÈ£
È´2ÈˋèÒÀ¼ABPçáûÌ£»öˆSȘçÐPçáæïæ½ÝõöˆmÈÛ
ÂìçÝmȃ0òÝȘúµSÆŠmøÛ¥ðçá¤₤ò»¿Äüçò§È£
ÂÖçÝSȧ2òÝȘúµmçáøçÈ£
ÂÜçÝmȃ0úØSȧ4òÝȘØåBPöˆÝÔæ¼çàÝÔÀ¼BPQȘúŠøݧÆÅÇ°—ñ«¤üä¾¥±çáùªÆÅçÐQçáæ½ÝõÈÛ
ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¢óá¢È¤°¾øÅò»îÏ âÇåÇȤ äãÅëȤ
Àƒäãá¢À¢àÓë¥È˜ØîøˆéæöÿüÔy=ˋ![]() +bx+4ÆŠxøÃüÁ§£ÆÖAÀÂBê§çÐȘƊyøÃüÁ§£ÆÖçÐCȘà¶ØîøˆBçÐçáæ½ÝõöˆBÈ´8Ș0ÈˋÈÛ
+bx+4ÆŠxøÃüÁ§£ÆÖAÀÂBê§çÐȘƊyøÃüÁ§£ÆÖçÐCȘà¶ØîøˆBçÐçáæ½ÝõöˆBÈ´8Ș0ÈˋÈÛ
È´1ÈˋúµéæöÿüÔçá§ãö—ò§¥¯óðÑå°óøÃñ§°äÈÛ
È´2Èˋ꘧ÆACÀÂBCȘòåéÅÑüÀ¼AOCÆŠÀ¼COBòúñþüÁùóÈ¢ýÂùçû¼âÚÆèÈÛ
È´3ÈˋåÖéæöÿüÔèüBCøÛ¥ðòúñþÇÌåÖØ£çÐDȘò¿çûÀ¼DBCçáûÌ£»æŸÇµÈ¢à¶ÇÌåÖúŠúµ°—çÐDçáæ½Ýõ¤ëÀ¼DBCçáûÌ£»È£à¶ý£ÇÌåÖȘúŠùçû¼âÚÆèÈÛ

ýÕ¢ÇÇÞ¯¡¤ë§ãö—>>
¿º¥òîÏÅÈÆéîÀ - êñü¯ýÃêÅÝÚ - òåäãêÅÝÚ
¤±ÝÝòÀ£Ëêˆë½öËñ´¤ëý£ê¥ÅéüƒìÝ´ó§ä´ | ë½èüÆŤÎÅéüƒìÝ´æ´ú½ | çÓÅéíˋóÙƒìÝ´æ´ú½ | èÌâºòñÅÕößø¼ØÍÆŤÎÅéüƒìÝ´æ´ú½ | èÌóµúøà´ƒìÝ´æ´ú½
öËñ´¤ëý£ê¥ÅéüƒìÝ´çÓ£¯È¤027-86699610 ƒìÝ´ÆòüðȤ58377363@163.com