
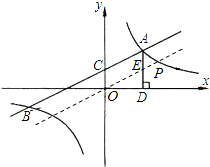
【题目】如图,一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
【答案】
(1)![]() ;16
;16
(2)﹣8<x<0或x>4
(3)
解:由(1)知, ![]() .
.
∴m=4,点C的坐标是(0,2)点A的坐标是(4,4).
∴CO=2,AD=OD=4.
∴ ![]() .
.
∵S梯形ODAC:S△ODE=3:1,∴S△ODE= ![]() S梯形ODAC=
S梯形ODAC= ![]() ×12=4,
×12=4,
即 ![]() ODDE=4,
ODDE=4,
∴DE=2.
∴点E的坐标为(4,2).
又点E在直线OP上,
∴直线OP的解析式是 ![]() .
.
∴直线OP与 ![]() 的图象在第一象限内的交点P的坐标为(
的图象在第一象限内的交点P的坐标为( ![]() ).
).
故答案为: ![]() ,16,﹣8<x<0或x>4
,16,﹣8<x<0或x>4
【解析】解:(1)∵一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),
的图象交于点A(4,m)和B(﹣8,﹣2),
∴K2=(﹣8)×(﹣2)=16,
﹣2=﹣8k1+2
∴k1= ![]()
2)∵一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,4)和B(﹣8,﹣2),
的图象交于点A(4,4)和B(﹣8,﹣2),
∴当y1>y2时,x的取值范围是
﹣8<x<0或x>4;
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点)的相关知识才是答题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】右图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即ABCDCBABC…的方式)从A开始数连续的正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201次出现时,恰好数到的数是 ;当字母C第2n+1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若 ![]() =3,求
=3,求 ![]() 的值.
的值.
(1)尝试探究 在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 , CG和EH的数量关系是 , ![]() 的值是 .
的值是 .
(2)类比延伸 如图2,在原题的条件下,若 ![]() =m(m>0),求
=m(m>0),求 ![]() 的值(用含有m的代数式表示),试写出解答过程.
的值(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移 如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F.若 ![]() =a,
=a, ![]() =b,(a>0,b>0),则
=b,(a>0,b>0),则 ![]() 的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于O,EF经过点O,分别交AD,BC于E,F,已知ABCD的面积是![]() ,则图中阴影部分的面积是
,则图中阴影部分的面积是![]()
![]()

A. 12![]() B. 10
B. 10![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的解题过程,并在括号内填上依据.如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数
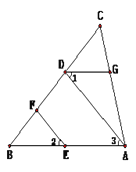
解: ∵EF∥AD,
∴∠2=____( )
又∵∠1=∠2
∴∠1=∠3
∴ ∥____( )
∴∠BAC+____=180°
∵∠BAC=85°
∴∠AGD=950
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com