
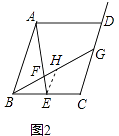
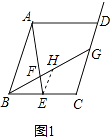
����Ŀ����ȡ�ת���������һ���˼�뷽��������ѧѧϰ���о��о����õ���������һ���������벹�������� ԭ�⣺��ͼ1����ƽ���ı���ABCD�У���E��BC���е㣬��F���߶�AE��һ�㣬BF���ӳ��߽�����CD�ڵ�G���� ![]() =3����
=3���� ![]() ��ֵ��
��ֵ��
��1������̽�� ��ͼ1�У�����E��EH��AB��BG�ڵ�H����AB��EH��������ϵ�� �� CG��EH��������ϵ�� �� ![]() ��ֵ�� ��
��ֵ�� ��
��2��������� ��ͼ2����ԭ��������£��� ![]() =m��m��0������
=m��m��0������ ![]() ��ֵ���ú���m�Ĵ���ʽ��ʾ������д�������̣�
��ֵ���ú���m�Ĵ���ʽ��ʾ������д�������̣�
��3����չǨ�� ��ͼ3������ABCD�У�DC��AB����E��BC���ӳ����ϵ�һ�㣬AE��BD�ཻ�ڵ�F���� ![]() =a��
=a�� ![]() =b����a��0��b��0������
=b����a��0��b��0������ ![]() ��ֵ�����ú�a��b�Ĵ���ʽ��ʾ����
��ֵ�����ú�a��b�Ĵ���ʽ��ʾ����
���𰸡�
��1��AB=3EH��CG=2EH��![]()
��2���⣺����ͼ2��ʾ����EH��AB��BG�ڵ�H�����EFH�ס�AFB��
�� ![]() =
= ![]() =m��
=m��
��AB=mEH��
��AB=CD��
��CD=mEH��
��EH��AB��CD��
���BEH�ס�BCG��
�� ![]() =2��
=2��
��CG=2EH��
�� ![]() =
= ![]() =
= ![]()
��3��ab
���������⣺��1�������⣬����E��EH��AB��BG�ڵ�H������ͼ1��ʾ�� ���С�ABF�ס�EHF��
�� ![]() ��
��
��AB=3EH��
��ABCD��EH��AB��
��EH��CD��
�֡�EΪBC�е㣬
��EHΪ��BCG����λ�ߣ�
��CG=2EH��![]() =
= ![]() =
= ![]() =
= ![]() ��
��
���Դ��ǣ�AB=3EH��CG=2EH�� ![]() ��
��
3������ͼ3��ʾ������E��EH��AB��BD���ӳ����ڵ�H������EH��AB��CD��
��EH��CD��
���BCD�ס�BEH��
�� ![]() =b��
=b��
��CD=bEH��
�� ![]() =a��
=a��
��AB=aCD=abEH��
��EH��AB��
���ABF�ס�EHF��
�� ![]() =
= ![]() =
= ![]() =ab��
=ab��
���Դ��ǣ�ab��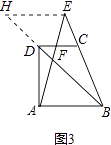
�����㾫����������Ҫ������ƽ���ı��ε����ʺ����εĶ�������֪ʶ�㣬��Ҫ����ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�һ��Ա�ƽ�У���һ��Ա߲�ƽ�е��ı��������Σ�������ȵ������ǵ������β�����ȷ�����⣮


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺�����������ع������ĵ�һ����5000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������![]() ����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±���ע������=�ۼ۩����ۣ�
����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±���ע������=�ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 20 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1�������ع������Ľ���һ�ι����ļס���������Ʒȫ�������һ���ɻ�ö�������
��2���ù������ĵڶ����Ե�һ�εĽ����ֹ����ס���������Ʒ�����м�����Ʒ�ļ������䣬������Ʒ�ļ����ǵ�һ�ε�3��������Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ���������Ʒ���������Ժ���������ȵ�һ�λ�õ��������160Ԫ����ڶ���������Ʒ�ǰ�ԭ�۴������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮������ijУ�ٰ��������й�ʫ�ʴ��������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱĬд50��ʫ�ʣ���ÿ��ȷĬд��һ��ʫ�ʵ�2�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ�� |
��1�� |
| 6 |
��2�� |
| 8 |
��3�� |
| 14 |
��4�� |
| a |
��5�� |
| 10 |
����ͼ��������и���
![]() �����a��ֵ��
�����a��ֵ��![]() Ƶ���ֲ�ֱ��ͼ����������
Ƶ���ֲ�ֱ��ͼ����������
![]() С������ݴ�ֱ��ͼ����һ������ͳ��ͼ�������������ɼ�Ϊ
С������ݴ�ֱ��ͼ����һ������ͳ��ͼ�������������ɼ�Ϊ![]() ��һ������Ӧ�����ε�Բ�ĽǵĶ�����
��һ������Ӧ�����ε�Բ�ĽǵĶ�����
![]() �����Գɼ�������80��Ϊ���㣬�β��Ե�������
�����Գɼ�������80��Ϊ���㣬�β��Ե�������![]() �ٷֱ�
�ٷֱ�![]() �Ƕ��٣�
�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OC�ǡ�AOB�ڲ���һ�����ߣ���AOC��30����OE�ǡ�COB��ƽ���ߣ�


��1����ͼ1������COE��40��ʱ�����AOB�Ķ�����
��2����OE��OAʱ������ͼ�л�������OE��OB����ֱ��д����AOB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬʱ�����90ǧ��A��ǰ��B�أ��׳�����������Ħ�г�������B��ͣ����Сʱ��A�أ���ͼ��������A�صľ���y��ǧ�ף���ʱ��x��ʱ��֮��ĺ�����ϵͼ�� 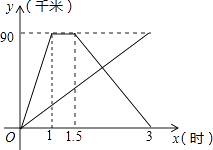
��1����״�B�ط���A�صĹ����У�y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2�����ҳ�����2Сʱ�ͼ����������Ҵ�A�ص�B�����˶ʱ�䣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺���������Ǻ͵������ǵ�ƽ���߶�Ӧ��ȵ�����������ȫ�ȣ����������ߺ͵��������ϵ����߶�Ӧ��ȵ�����������ȫ�ȣ����������ߺ͵��������ϵĸ߶�Ӧ��ȵ�����������ȫ�ȣ�������ȷ���ǣ�������
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
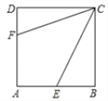
����Ŀ����ͼ��������ABCD�ı߳�Ϊ6����E��F�ֱ���AB��AD������CE=3![]() ���ҡ�ECF=45�㣬��CF��Ϊ�� ��
���ҡ�ECF=45�㣬��CF��Ϊ�� ��
A. 2![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y1=k1x+2�뷴�������� ![]() ��ͼ���ڵ�A��4��m����B����8����2������y�ύ�ڵ�C��
��ͼ���ڵ�A��4��m����B����8����2������y�ύ�ڵ�C��
��1��k1= �� k2=��
��2�����ݺ���ͼ���֪����y1��y2ʱ��x��ȡֵ��Χ����
��3������A��AD��x���ڵ�D����P�Ƿ����������ڵ�һ����ͼ����һ�㣮��ֱ��OP���߶�AD���ڵ�E����S�ı���ODAC��S��ODE=3��1ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����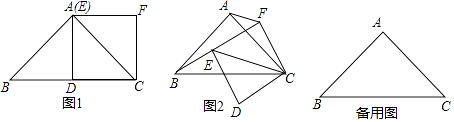
��1�������ⷢ�֡�
��ͼ1����Rt��ABC�У�AB=AC=2����BAC=90�㣬��DΪBC���е㣬��CDΪһ����������CDEF����Eǡ�����A�غϣ����߶�BE��AF��������ϵΪ
��2������չ�о���
�ڣ�1���������£����������CDEF�Ƶ�C��ת������BE��CE��AF���߶�BE��AF��������ϵ���ޱ仯�������ͼ2�����θ���֤����
��3�������ⷢ�֡�
��������CDEF��ת��B��E��F���㹲��ʱ��ֱ��д���߶�AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com