
【题目】已知OC是∠AOB内部的一条射线,∠AOC=30°,OE是∠COB的平分线.


(1)如图1,当∠COE=40°时,求∠AOB的度数;
(2)当OE⊥OA时,请在图中画出射线OE,OB,并直接写出∠AOB的度数.
【答案】(1) 110°;(2)作图见解析, ∠AOB=150°.
【解析】试题分析:(1)由OE为角平分线,得到∠COB=2∠COE,由![]() 的度数求出∠COB的度数,再由∠AOB=∠AOC+∠COB即可求出∠AOB的度数;
的度数求出∠COB的度数,再由∠AOB=∠AOC+∠COB即可求出∠AOB的度数;
(2)作出相应的图形,如图所示,由OE垂直于OA,根据∠AOC度数求出∠EOC 的度数,同理可得出∠AOB的度数.
解:(1)∵OE是∠COB的平分线(已知),
∴∠COB=2∠COE(角平分线定义).
∵∠COE=40°,
∴∠COB=80°.
∵∠AOC=30°,
∴∠AOB=∠AOC+∠COB=110°.
(2)如右图:

∵∠AOC=30°,OE⊥OA,
∴∠COE=60°.
∵OE是∠COB的平分线,
∴∠COB=2∠COE=120°.
∵∠AOC=30°,
∴∠AOB=∠AOC+∠COB=30°+120°=150°.


科目:初中数学 来源: 题型:
【题目】某餐厅计划购买12张餐桌和一批椅子(不少于12把),现从甲、乙两商场了解到同一型号的餐桌报价都为每张200元,餐椅报价都为每把50元.甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八五折销售,那么,什么情况下到甲商场购买更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即ABCDCBABC…的方式)从A开始数连续的正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201次出现时,恰好数到的数是 ;当字母C第2n+1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A, ![]() .则下列结论中不一定正确的是( )
.则下列结论中不一定正确的是( ) 
A.BA⊥DA
B.OC∥AE
C.∠COE=2∠CAE
D.OD⊥AC
查看答案和解析>>
科目:初中数学 来源: 题型:
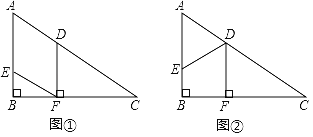
【题目】如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒lcm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(I)试用含t的式子表示AE、AD、DF的长;
(Ⅱ)如图①,连接EF,求证:四边形AEFD是平行四边形;
(Ⅲ)如图②,连接DE,当t为何值时,四边形EBFD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若 ![]() =3,求
=3,求 ![]() 的值.
的值.
(1)尝试探究 在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 , CG和EH的数量关系是 , ![]() 的值是 .
的值是 .
(2)类比延伸 如图2,在原题的条件下,若 ![]() =m(m>0),求
=m(m>0),求 ![]() 的值(用含有m的代数式表示),试写出解答过程.
的值(用含有m的代数式表示),试写出解答过程.
(3)拓展迁移 如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F.若 ![]() =a,
=a, ![]() =b,(a>0,b>0),则
=b,(a>0,b>0),则 ![]() 的值是(用含a、b的代数式表示).
的值是(用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com