
����Ŀ��С����ѧϰ������֪ʶʱ����������������Ȥ�Ľ��ۣ���Rt��ABC�У���A��90�㣬BDƽ�֡�ABC��MΪֱ��AC��һ�㣬ME��BC������ΪE����AME��ƽ���߽�ֱ��AB�ڵ�F��
��1����ͼ�٣�MΪ��AC��һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ڣ�MΪ��AC�����ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��ͼ�ۣ�MΪ��AC�ӳ�����һ�㣬��BD��MF��λ�ù�ϵ�� ��
��2�����ͼ�١�ͼ�ڡ���ͼ���е�һ�����������֤��.

���𰸡���1��BD��MF��BD��MF��BD��MF����2��֤����������
��������
���⣨1��ƽ�У���ֱ����ֱ�� 3��
��2��ѡ�� ֤��BD��MF
�������£��ߡ�A=90����ME��BC��
���ABC+��AME=360�㩁90���2=180���� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=![]() ��ABC����AMF=
��ABC����AMF=![]() ��AME��
��AME��
���ABD+��AMF=![]() ����ABC+��AME��=90���� 2��
����ABC+��AME��=90���� 2��
���ߡ�AFM+��AMF=90����
���ABD=��AFM�� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��C=��AME+��C=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�ABD+��ADB=90����
���AMF+��ADB=90���� 3��
��BD��MF�� 4��
ѡ�� ֤��BD��MF��
�������£��ߡ�A=90����ME��BC��
���ABC+��ACB=��AME+��ACB=90����
���ABC=��AME�� 1��
��BDƽ����ABC��MFƽ����AME��
���ABD=��AMF�� 2��
�ߡ�AMF+��F=90����
���ABD+��F=90���� 3��
��BD��MF�� 4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABCD�У�![]() ��
��![]() �Ƶ�A˳ʱ����ת���������߳��ֱ�CB��DC�����ǵ��ӳ���
�Ƶ�A˳ʱ����ת���������߳��ֱ�CB��DC�����ǵ��ӳ���![]() �ڵ�MN��
�ڵ�MN��![]() �ڵ�H��
�ڵ�H��
![]() ��ͼ
��ͼ![]() ����
����![]() ��A��ת��
��A��ת��![]() ʱ������ֱ��д��AH��AB��������ϵ��
ʱ������ֱ��д��AH��AB��������ϵ��
![]() ��ͼ
��ͼ![]() ����
����![]() �Ƶ�A��ת��
�Ƶ�A��ת��![]() ʱ��
ʱ��![]() �з��ֵ�AH��AB��������ϵ�������������������д�����ɣ����������֤����
�з��ֵ�AH��AB��������ϵ�������������������д�����ɣ����������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��2��3����˫����y= ![]() ��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��1����k��ֵ����E�����ꣻ
��2������F��OC����һ�㣬�ҡ�FBC�ס�DEB����ֱ��FB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
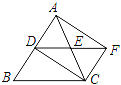
����Ŀ����ͼ������BC�У�AC=BC����D��E�ֱ��DZ�AB��AC���е㣮�ӳ�DE����F��ʹDE=EF�����ı���ADCF����ʹ�ı���ADCF�������Σ���Ӧ����ABC��������һ������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OC�ǡ�AOB�ڲ���һ�����ߣ���AOC��30����OE�ǡ�COB��ƽ���ߣ�


��1����ͼ1������COE��40��ʱ�����AOB�Ķ�����
��2����OE��OAʱ������ͼ�л�������OE��OB����ֱ��д����AOB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ
��1��2x��{��3y��[3x��2(3x��y)]}������x����1��y��![]() ��
��
��2��5(3a2b��ab2��1)��(ab2��3a2b��5)������a��![]() ��b��
��b��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺���������Ǻ͵������ǵ�ƽ���߶�Ӧ��ȵ�����������ȫ�ȣ����������ߺ͵��������ϵ����߶�Ӧ��ȵ�����������ȫ�ȣ����������ߺ͵��������ϵĸ߶�Ӧ��ȵ�����������ȫ�ȣ�������ȷ���ǣ�������
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ�ڼ���һ�������(ÿ���ڽ�С��180��)���ڽǺ�ʱ�����ڴ���������һ���ڽǣ�
����õ����ܺ���2018�㣬������������ڽǵĶ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
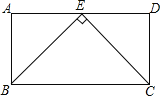
����Ŀ����ͼ���ھ���ABCD�У�E��AD���е㣬��![]() ������ABCD���ܳ�Ϊ48cm�������ABCD�����Ϊ______
������ABCD���ܳ�Ϊ48cm�������ABCD�����Ϊ______![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com