
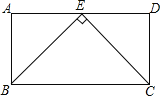
【题目】如图,在矩形ABCD中,E是AD的中点,且![]() 若矩形ABCD的周长为48cm,则矩形ABCD的面积为______
若矩形ABCD的周长为48cm,则矩形ABCD的面积为______![]() .
.
【答案】128
【解析】
根据AB=DC,∠A=∠D,AE=DE,利用SAS可判定△ABE≌△DCE,根据全等三角形的性质可得:∠AEB=∠DEC,再根据BE⊥CE,可得:∠BEC=90°,进而可得:∠AEB=∠DEC=45°,
因此∠EBC=∠ECD=45°,继而可得:AB=AE,DC=DE,即AD=2AB,根据周长=48,可求得:BC=16,AB=8,最后根据矩形面积公式计算可得:S=16×8=128 cm.
∵AB=DC,∠A=∠D,AE=DE,
∴△ABE≌△DCE(SAS),
∴∠AEB=∠DEC,
∵BE⊥CE,
∴∠BEC=90°,
∵∠AEB+∠BEC+∠DEC=180°,
∴∠AEB=∠DEC=45°,
∴∠EBC=∠ECD=45°,
∴AB=AE,DC=DE,
即AD=2AB,
又∵周长=48,
∴BC=16,AB=8,
S=16×8=128 cm,
故答案为:128.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于O,EF经过点O,分别交AD,BC于E,F,已知ABCD的面积是![]() ,则图中阴影部分的面积是
,则图中阴影部分的面积是![]()
![]()

A. 12![]() B. 10
B. 10![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-![]() ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
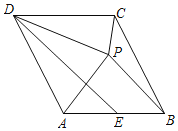
【题目】在菱形ABCD中,![]() ,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:
,点E为AB边的中点,点P与点A关于DE对称,连接DP、BP、CP,下列结论:![]() ;
;![]() ;
;![]() ;
;![]() ,其中正确的是
,其中正确的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
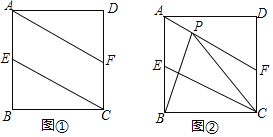
【题目】如图![]() ,矩形ABCD中,
,矩形ABCD中,![]() ,
,![]() ,E、F分别是AB、CD的中点
,E、F分别是AB、CD的中点
![]() 求证:四边形AECF是平行四边形;
求证:四边形AECF是平行四边形;
![]() 是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
是否存在a的值使得四边形AECF为菱形,若存在求出a的值,若不存在说明理由;
![]() 如图
如图![]() ,点P是线段AF上一动点且
,点P是线段AF上一动点且![]()
![]() 求证:
求证:![]() ;
;
![]() 直接写出a的取值范围.
直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=![]() ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
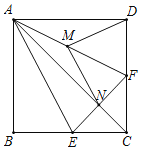
【题目】操作与证明:如图,把一个含![]() 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、![]() 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 在
在![]() 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com