
����Ŀ����ƽ��ֱ������ϵ�У���֪������y��![]() x2+kx+c��ͼ����C��0��1������x��2ʱ����������Сֵ��
x2+kx+c��ͼ����C��0��1������x��2ʱ����������Сֵ��
��1���������ߵĽ���ʽ��
��2��ֱ��l��y�ᣬ��������Ϊ��0����1���������ߵĶԳ�����ֱ��l���ڵ�A����x������һ��B����AB��![]() ������ֱ��l�������ڵ�A��һ��Q��ʹ��Q�ڡ�ABC�����Բ�ϣ�
������ֱ��l�������ڵ�A��һ��Q��ʹ��Q�ڡ�ABC�����Բ�ϣ�
��3����P��a��b��Ϊ��������һ���㣬��MΪ����ϵ��һ���㣬����P��ֱ��l�ľ���ʼ�յ����߶�PM�ij�����M�����꣮
���𰸡���1��y��![]() x2��x+1�� ��2��Q��1����1������3��M��2��1��
x2��x+1�� ��2��Q��1����1������3��M��2��1��
��������
��1������֪���������߽���ʽΪy��![]() x2��x+1��
x2��x+1��
��2���������֪A��2����1������B��t��0������AB��![]() �����ԣ�t��2��2+1��2�����B��1��0����B��3��0������B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ������B��3��0������֤����ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨
�����ԣ�t��2��2+1��2�����B��1��0����B��3��0������B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ������B��3��0������֤����ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨![]() ��
��![]() �����뾶Ϊ
�����뾶Ϊ![]() ����Q��x����1�������У�x��
����Q��x����1��������x��![]() ��2+��
��2+��![]() +1��2����
+1��2����![]() ��2��������Q��1����1����
��2��������Q��1����1����
��3���趥��M��m��n����P��a��b��Ϊ��������һ���㣬����b��![]() a2��a+1����ΪP��ֱ��l�ľ������PM�����ԣ�m��a��2+��n��b��2����b+1��2���ɵ�
a2��a+1����ΪP��ֱ��l�ľ������PM�����ԣ�m��a��2+��n��b��2����b+1��2���ɵ�![]() +��2n��2m+2��a+��m2+n2��2n��3����0����aΪ����ֵ������ʽ����������
+��2n��2m+2��a+��m2+n2��2n��3����0����aΪ����ֵ������ʽ����������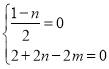 ������M�����꣮
������M�����꣮
�⣺��1����ͼ����C��0��1����
��c��1��
�ߵ�x��2ʱ����������Сֵ�����Գ���Ϊֱ��x��2��
��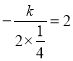 ����ã�k����1��
����ã�k����1��
�������߽���ʽΪy��![]() x2��x+1��
x2��x+1��
��2���������֪A��2����1������B��t��0����
��AB��![]() ��
��
�ࣨt��2��2+1��2��
��t��1��t��3��
��B��1��0����B��3��0����
��B��1��0��ʱ��A��B��C���㹲�ߣ���ȥ��
��B��3��0����
��AC��2![]() ��BC��
��BC��![]() ��
��
���BAC��90�㣬
���ABCΪֱ�������Σ�BCΪ���Բ��ֱ�������Բ��Բ��ΪBC���е㣨![]() ��
��![]() �����뾶Ϊ
�����뾶Ϊ![]() ��
��
��Q��x����1��������x��![]() ��2+��
��2+��![]() +1��2����
+1��2����![]() ��2��
��2��
��x��1��x��2����ȥ����
��Q��1����1����
��3���趥��M��m��n������P��a��b��Ϊ��������һ���㣬
��b��![]() a2��a+1��
a2��a+1��
��P��ֱ��l�ľ������PM��
�ࣨm��a��2+��n��b��2����b+1��2��
��![]() +��2n��2m+2��a+��m2+n2��2n��3����0��
+��2n��2m+2��a+��m2+n2��2n��3����0��
��aΪ����ֵ������ʽ��������
��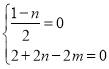 ��
��
��![]() ��
��
��ʱm2+n2��2n��3��0��
�ඨ��M��2��1����


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3�֣���ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽���AB��D�㣬����AC��E�㣬����ABC����EBC���ܳ��ֱ���40cm��24cm����AB= cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
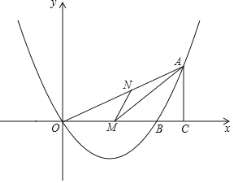
����Ŀ����ͼ����֪���κ��� y��ax2+bx ��ͼ���� x �ύ�ڵ� O��0��0���� �� B�������ߵĶԳ�����ֱ�� x��3���� A ���������ڵ�һ�����ϵ�һ�����㣬 ���� A �� AC��x �ᣬ����Ϊ C��S��AOB��3S��ABC��AC2��OCBC��
��1����ö��κ����Ľ���ʽ��
��2�������ߵĶԳ����� x �ύ�ڵ� M������ AM���� N ���߶� OA �ϵ�һ�㣮�� ��AMN����AOM ʱ����� N �����ꣻ
��3���� P ���������ϵ�һ�����㣮�� Q �� y ���ϵ�һ���㣮���� A��B��P��Q �ĸ���Ϊ������ı���Ϊƽ���ı���ʱ��ֱ��д���� P ���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
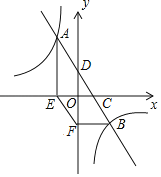
����Ŀ����ͼ����֪һ�κ���y����2x+b�뷴��������y��![]() ��ͼ������������A��m��3����B����һ�κ���y����2x+b��x�ᡢy��ֱ��ڵ�C��D������A��AE��x���ڵ�E������B��BF��y���ڵ�F����F������Ϊ��0����2��������EF��tan��FEO��2��
��ͼ������������A��m��3����B����һ�κ���y����2x+b��x�ᡢy��ֱ��ڵ�C��D������A��AE��x���ڵ�E������B��BF��y���ڵ�F����F������Ϊ��0����2��������EF��tan��FEO��2��
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ı���AEFD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������y����![]() ��x��1��2+5��ͼ��Ҫ���б�����㣩���ش��������⣺
��x��1��2+5��ͼ��Ҫ���б�����㣩���ش��������⣺
��1��д�����Ŀ��ڷ��Գ���Ͷ������ꣻ
��2����y��x�����������ʱ��д��x��ȡֵ��Χ��
��3������������x����㣨x1��0������n��x1��n+1����nΪ����������д��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������߾���A��-1��0����B��3��0�����C��0��3��������BC����P��ֱ��BC���Ϸ���һ�����㣨�Ҳ���B��C�غϣ���
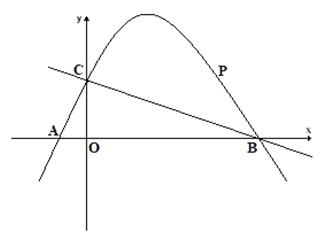
��1���������ߵĽ���ʽ��
��2������PBC����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC�У�OA��3��AB��4��˫����![]() ��k��0�����������AB��BC�ֱ���D��E����BD��2AD
��k��0�����������AB��BC�ֱ���D��E����BD��2AD
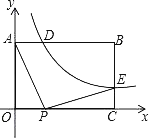
��1����k��ֵ�͵�E�����ꣻ
��2����P���߶�OC�ϵ�һ�����㣬�Ƿ���ڵ�P��ʹ��APE��90�㣿�����ڣ������ʱ��P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ���κ���y=-x2+bx+c��ͼ����ͼ��ʾ�����м������ۣ��ٶԳ���Ϊֱ��x=2���ڵ�y��0ʱ��x��0��x��4���ۺ�������ʽΪy=-x2+4x���ܵ�x��0ʱ��y��x�����������������ȷ�Ľ����У�������
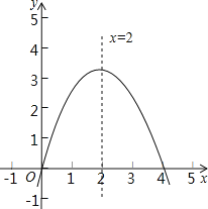
A.�٢ڢۢ�B.�٢ڢ�C.�٢ۢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
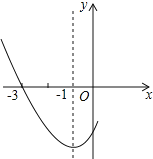
����Ŀ����ͼ���Ƕ��κ���![]() ͼ���һ���֣���Գ�����
ͼ���һ���֣���Գ�����![]() ���ҹ���
���ҹ���![]() ������˵����
������˵����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �������������㣬��
�������������㣬��![]() ��������ȷ����
��������ȷ����![]() ����
����![]()
A. 1��
B. 2��
C. 3��
D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com