
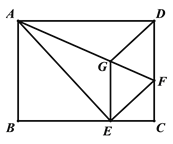
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)若AG=7、GF=3,求DF的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接DE交AF于H,先根据DF=EG,DF∥EG,判定四边形DFEG是平行四边形,再根据GF⊥DE,即可得出四边形EFDG是菱形;
(2)根据条件得到FH=![]() GF=
GF=![]() ,AF=10,再根据Rt△ADF中,DH⊥AF,运用射影定理即可得到DF2=FH×FA,进而得出DF的长.
,AF=10,再根据Rt△ADF中,DH⊥AF,运用射影定理即可得到DF2=FH×FA,进而得出DF的长.
试题解析: (1)如图,连接DE交AF于H,

由折叠可得,AF⊥DE,DF=EF,∠DFG=∠EFG,
∵EG∥CD,
∴∠DFG=∠EGF,
∴∠EFG=∠EGF,
∴EG=EF,
∴DF=EG,
∵DF∥EG,
∴四边形DFEG是平行四边形,
∵GF⊥DE,
∴四边形EFDG是菱形;
(2)∵四边形EFDG是菱形,
∴FH=![]() GF=
GF=![]() ,
,
∵AG=7,GF=3,
∴AF=10,
∵Rt△ADF中,DH⊥AF,
∴DF2=FH×FA,
即DF=![]() =
=![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】观察下表三行数的规律,回答下列问题:
第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(1)第1行的第四个数a是 ;第3行的第六个数b是 ;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为 ;
(3)已知第n列的三个数的和为2562,若设第1行第n列的数为x,试求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
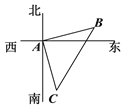
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水稻种植是嘉兴的传统农业.为了比较甲、乙两种水稻秧苗的长势,农技人员从两块试验田中分别随机抽取5株水稻秧苗,将测得的苗高数据绘制成如图所示的统计图.
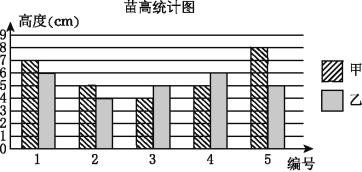
请你根据统计图所提供的数据,计算甲、乙两种水稻苗高的平均数和方差,并比较两种水稻的长势.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,代数式
时,代数式![]() 的值是5,求当
的值是5,求当![]() 时,代数式px3+qx+1的值;
时,代数式px3+qx+1的值;
(3)当![]() 时,代数式
时,代数式![]() 的值为m,求当
的值为m,求当![]() 时,求代数式
时,求代数式![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“摩拜单车”公司调查无锡市民对其产品的了解情况,随机抽取部分市民进行问卷,结果分“非常了解”、“比较了解”、“一般了解”、“不了解”四种类型,分别记为![]() 、
、![]() 、
、![]() 、
、![]() .根据调查结果绘制了如下尚不完整的统计图.
.根据调查结果绘制了如下尚不完整的统计图.
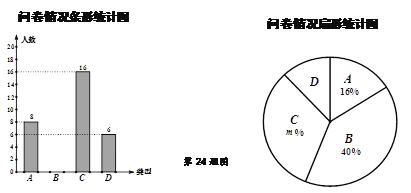
(1)本次问卷共随机调查了 名市民,扇形统计图中![]() .
.
(2)请根据数据信息补全条形统计图.
(3)扇形统计图中“D类型”所对应的圆心角的度数是 .
(4)从这次接受调查的市民中随机抽查一个,恰好是“不了解”的概率是 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两个点所对应的数的差的绝对值.例:点A、B在数轴上对应的数分别为a、b,则A、B两点间的距离表示为AB=|a﹣b|.根据以上知识解题:
(1)点A在数轴上表示3,点B在数轴上表示2,那么AB=_______.
(2)在数轴上表示数a的点与﹣2的距离是3,那么a=______.
(3)如果数轴上表示数a的点位于﹣4和2之间,那么|a+4|+|a﹣2|=______.
(4)对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接写出最小值.如果没有.请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com