
 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.分析 (1)连接OB,由E为OD中点,得到OE等于OA的一半,在直角三角形AOE中,得出∠OAB=30°,进而求出∠AOE与∠AOB的度数,设OA=x,利用勾股定理求出x的值,确定出圆的半径,利用弧长公式即可求出$\widehat{AB}$的长;
(2)由第一问得到∠BAM=∠BMA,利用等角对等边得到AB=MB,利用SAS得到三角形OCM与三角形OBM全等,利用全等三角形对应边相等得到CM=BM,等量代换得到CM=AB,再利用全等三角形对应角相等及等量代换得到一对内错角相等,进而确定出CM与AB平行,利用一组对边平行且相等的四边形为平行四边形得到ABMC为平行四边形,最后由邻边相等的平行四边形为菱形即可得证.
解答  (1)解:∵OA=OB,E为AB的中点,
(1)解:∵OA=OB,E为AB的中点,
∴∠AOE=∠BOE,OE⊥AB,
∵OE⊥AB,E为OD中点,
∴OE=$\frac{1}{2}$OD=$\frac{1}{2}$OA,
∴在Rt△AOE中,∠OAB=30°,∠AOE=60°,∠AOB=120°,
设OA=x,则OE=$\frac{1}{2}$x,AE=$\frac{\sqrt{3}}{2}$x,
∵AB=4$\sqrt{3}$,
∴AB=2AE=$\sqrt{3}$x=4$\sqrt{3}$,
解得:x=4,
则$\widehat{AB}$的长l=$\frac{120π×4}{180}$=$\frac{8π}{3}$;
(2)证明:由(1)得∠OAB=∠OBA=30°,∠BOM=∠COM=60°,∠AMB=30°,
∴∠BAM=∠BMA=30°,
∴AB=BM,
∵BM为圆O的切线,
∴OB⊥BM,
在△COM和△BOM中,
$\left\{\begin{array}{l}{OC=OB}\\{∠COM=∠BOM}\\{OM=OM}\end{array}\right.$,
∴△COM≌△BOM(SAS),
∴CM=BM,∠CMO=∠BMO=30°,
∴CM=AB,∠CMO=∠MAB,
∴CM∥AB,
∴四边形ABMC为菱形.
点评 此题考查了切线的性质,菱形的判断,全等三角形的判定与性质,以及弧长公式,熟练掌握切线的性质是解本题的关键.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:填空题
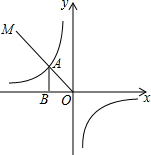 如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.
如图所示,第二象限的角平分线OM与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,已知OA=3$\sqrt{2}$,则k=-9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
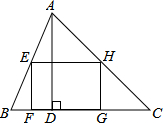 如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.
如图,矩形EFGH内接于△ABC,且边FG落在BC上.若BC=3,AD=2,EF=$\frac{2}{3}$EH,那么EH的长为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
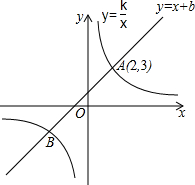 如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).
如图,已知一次函数y=x+b与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,其中点A的坐标为(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
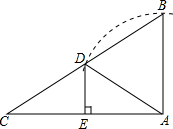 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.
如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
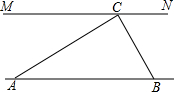 为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
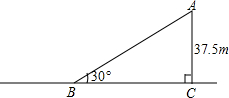 一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.
一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com