
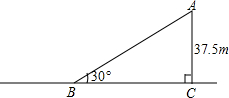
 一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.
一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.分析 (1)由∠B=30°,得到AB=2AC=75m,由速度每秒增加1.5m/s,根据公式v02=2aAB,计算出v0即可;
(2)根据公式S=v0t+$\frac{1}{2}$at2=v0t-6t2,求出a,然后求出刹车时间,再求刹车距离即可.
解答 解:(1)∵∠B=30°,∠ACB=90°,
∴AB=75m,
∵加速度a=1.5m/s2,v02=2aAB,
∴v0=15m/s;
(2)∵S=v0t+$\frac{1}{2}$at2=v0t-6t2,
∴a=-125m/s2,
∴刹车时间t=$\frac{0m/s-15m/s}{-12m/{s}^{2}}$=$\frac{5}{4}$s,
∴刹车距离为:S=v0t-6t2,=15×$\frac{5}{4}$-6×($\frac{5}{4}$)2=9.375(m),
故驾驶员至少需要在距路中行人9.375m处开始刹车.
点评 本题主要考查了实际应用问题,专业性较强,关键要知道加速度公式才能更好地理解题意来解决问题.


科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
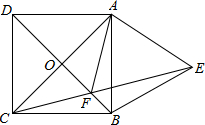 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
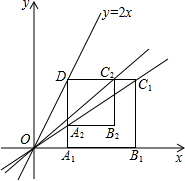 如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.
如图,在平面直角坐标系xOy中,点D为直线y=2x上且在第一象限内的任意一点,DA1⊥x轴于点A1,以DA1为边在DA1的右侧作正方形A1B1C1D;直线OC1与边DA1交于点A2,以DA2为边在DA2的右侧作正方形A2B2C2D;直线OC2与边DA1交于点A3,以DA3为边在DA3的右侧作正方形A3B3C3D,…,按这种方式进行下去,则直线OC1对应的函数表达式为y=$\frac{2}{3}$x,直线OC3对应的函数表达式为y=$\frac{14}{15}x$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
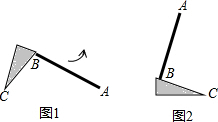 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com