
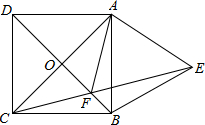
 已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$.
已知正方形ABCD的对角线AC,BD相交于点O,以AB为边向外作等边三角形ABE,CE与BD相交于点F,则$\frac{OA}{OF}$的值为$\sqrt{3}$. 分析 由正方形的性质和等边三角形的性质可知∠CBE=150°,因为BC=BE,所以∠ECB=15°,从而可知:∠FAB=15°,然后可证明∠OAF=30°,最后利用特殊锐角三角函数即可求得答案.
解答 解:∵四边形ABCD是正方形,三角形ABE为等边三角形,
∴BC=BE,∠CBE=150°.
∴∠ECB=∠CEB=15°.
由正方形的对称性可知:∠ECB=∠AFB=15°,
∴∠OAF=∠CAB-∠FAB=45°-15°=30°.
由特殊锐角三角函数值可知:$\frac{OA}{OF}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题主要考查的是正方形的性质和等边三角形的性质和等腰三角形的性质,求得∠OAF的度数是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
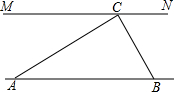 为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-3 | B. | x≠5 | C. | x≥-3或x≠5 | D. | x≥-3且x≠5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
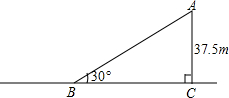 一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.
一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )
如图在△ABC中,∠C=90°,BC=6,D、E分别在AB、AC上,将△ADE沿DE翻折后,点A落在CE的中点A′处,则折痕DE的长为( )| A. | 1 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
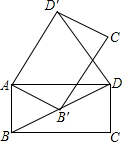 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com