

分析 操作发现:由条件可以通过三角形全等和轴对称的性质,直角三角形斜边上的中线性质以及四点共圆即可得出结论;
数学思考:取AB、AC的中点F、G,连接DF,MF,EG,MG,根据三角形的中位线的性质和等腰直角三角形的性质就可以得出四边形AFMG是平行四边形,从而得出△DFM≌△MGE,根据其性质以及各个角之间的关系即可得出结论;
类比探索:取AB、AC的中点F、G,连接DF,MF,EG,MG,DF和MG相交于H,根据三角形的中位线的性质K可以得出△DFM≌△MGE,由全等三角形的性质就可以得出结论.
解答 操作发现:
解:∵△ADB和△AEC是等腰直角三角形,
∴∠ABD=∠DAB=∠ACE=∠EAC=45°,∠ADB=∠AEC=90°
∵在△ADB和△AEC中,
$\left\{\begin{array}{l}{∠ABD=∠ACE}\\{∠ADB=∠AEC}\\{AB=AC}\end{array}\right.$,
∴△ADB≌△AEC(AAS),
∴BD=CE,AD=AE,
∵DF⊥AB于点F,EG⊥AC于点G,
∴AF=BF=DF=$\frac{1}{2}$AB,AG=GC=GE=$\frac{1}{2}$AC.
∵AB=AC,
∴AF=AG=$\frac{1}{2}$ AB,故①正确;
∵M是BC的中点,
∴BM=CM.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC+∠ABD=∠ACB+∠ACE,
即∠DBM=∠ECM.
在△DBM和△ECM中,
$\left\{\begin{array}{l}{BD=CE}\\{∠DBM=∠ECM}\\{BM=CM}\end{array}\right.$,
∴△DBM≌△ECM(SAS),
∴MD=ME.故②正确;
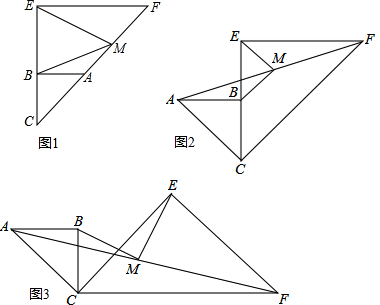
连接AM、FM、GM,如图1所示: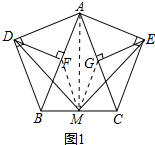 ∵AB=AC,M是BC的中点,
∵AB=AC,M是BC的中点,
∴AM⊥BC,
∴∠AMB=∠AMC=90°,
又∵AF=BF,AG=CG,
∴FM=$\frac{1}{2}$AB=AF,GM=$\frac{1}{2}$AC=AG,
∴AF=FM=GM=AG,
∴四边形AFMG是菱形,
故③正确;
根据前面的证明可以得出将图形1,沿AM对折左右两部分能完全重合,
∴整个图形是轴对称图形,故④正确.
∵AB=AC,BM=CM,
∴AM⊥BC,
∴∠AMB=∠AMC=90°,
∵∠ADB=90°,
∴四边形ADBM四点共圆,
∴∠AMD=∠ABD=45°.
∵AM是对称轴,
∴∠AME=∠AMD=45°,
∴∠DME=90°,
∴MD⊥ME,故⑤正确,
数学思考:
解:MD=ME,MD⊥ME;理由如下:
取AB、AC的中点F、G,连接DF,MF,EG,MG,如图2所示: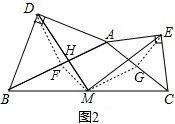
∴AF=$\frac{1}{2}$AB,AG=$\frac{1}{2}$AC.
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=$\frac{1}{2}$AB,EG⊥AC,EG=$\frac{1}{2}$ AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
∵在△DFM和△MGE中,
$\left\{\begin{array}{l}{MF=GE}\\{∠DFM=∠MGE}\\{DF=MG}\end{array}\right.$,
∴△DFM≌△MGE(SAS),
∴DM=ME,∠FMD=∠GEM,
∴∠DME=∠FMG-(∠FMD+∠GME)=∠MGC-(∠GEM+∠GME),
∵EG⊥AC,
∴∠EGC=90°,
∵∠MGC-(∠GEM+∠GME)+∠EGC=180°,
∴∠DME=90°,
∴DM⊥EM;
类比探索:
解:取AB、AC的中点F、G,连接DF,MF,EG,MG,如图3所示: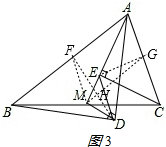 ∵点M、F、G分别是BC、AB、AC的中点,
∵点M、F、G分别是BC、AB、AC的中点,
∴MF∥AC,MF=$\frac{1}{2}$ AC,MG∥AB,MG=$\frac{1}{2}$ AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG.∠AFM=∠AGM.
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
$\left\{\begin{array}{l}{MF=EG}\\{∠DFM=∠MGE}\\{DF=MG}\end{array}\right.$,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
点评 本题是四边形综合题目,考查了等腰直角三角形的性质、等腰三角形的性质、全等三角形的判定及性质、三角形的中位线的性质、直角三角形的斜边上的中线的性质、平行四边形的判定及性质等知识;本题难度较大,综合性强,需要通过作辅助线证明三角形全等、证明平行四边形、四点共圆才能得出结论.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:填空题
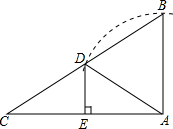 如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.
如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为(6+2$\sqrt{3}$)a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
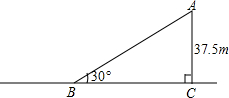 一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.
一辆汽车从斜坡顶端A处由静止开始沿斜坡滑下,速度每秒增加1.5m/s,已知斜坡高37.5m,坡角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
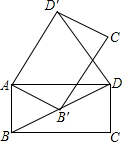 如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$.将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$+1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
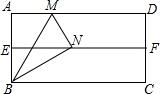 数学兴趣小组开展以下折纸活动:
数学兴趣小组开展以下折纸活动:| A. | 25° | B. | 30° | C. | 36° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com