
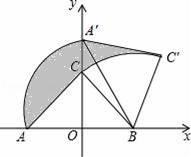
如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )

A.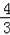
 π﹣2 B.
π﹣2 B.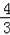
 π C.
π C.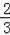
 π D.
π D.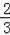
 π﹣2
π﹣2
C【分析】根据等腰直角三角形的性质求出AB,再根据旋转的性质可得A′B=AB,然后求出∠OA′B=30°,再根据直角三角形两锐角互余求出∠A′BA=60°,即旋转角为60°,再根据S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′=S扇形ABA′﹣S扇形CBC′,然后利用扇形的面积公式列式计算即可得解.
【解答】解:∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∴AB=2OA=2OB=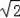
 AC=2
AC=2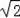
 ,
,
∵△ABC绕点B顺时针旋转点A在A′处,
∴BA′=AB,
∴BA′=2OB,
∴∠OA′B=30°,
∴∠A′BA=60°,
即旋转角为60°,
S阴影=S扇形ABA′+S△A′BC′﹣S△ABC﹣S扇形CBC′,
=S扇形ABA′﹣S扇形CBC′,
=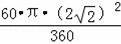
 ﹣
﹣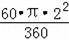
 ,
,
=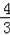
 π﹣
π﹣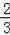
 π,
π,
=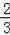
 π.
π.
故选C.
【点评】本题考查了旋转的性质,等腰直角三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,表示出阴影部分的面积等于两个扇形的面积的差是解题的关键,难点在于求出旋转角的度数.


科目:初中数学 来源: 题型:
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
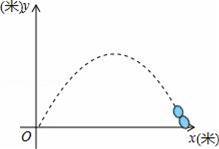

A.4米 B.3米 C.2米 D.1米
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,
(1)求抛物线所对应的函数解析式;
(2)求△ABD的面积;
(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
有这样一组数据a1,a2,a3,…an,满足以下规律:a1=
 、a2=
、a2=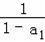
 、a3=
、a3=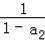
 、…、an=
、…、an=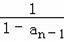
 (n≥2,且n为正整数),则a2015的值为 (结果用数字表示).
(n≥2,且n为正整数),则a2015的值为 (结果用数字表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
|
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com