
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>a m2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
m2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
A.①②③ B.②④ C.②⑤ D.②③⑤

科目:初中数学 来源: 题型:
四川省第十二届运动会将于2014年8月18日在我市隆重开幕,根据大会组委会安排,某校接受了开幕式大型团体操表演任务.为此,学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2 200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.
(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;
(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,一次函数y=x+1的图象与反比例函数y= (k≠0)的图象都经过点A(a,2).
(k≠0)的图象都经过点A(a,2).
(1)求a的值及反比例函数的表达式;
(2)判断点B(2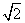 ,
,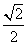 )是否在该反比例函数的图象上,请说明理由.
)是否在该反比例函数的图象上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,反比例函数y= 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).
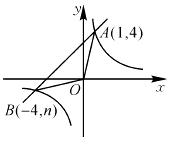
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
若抛物线y=x2-2x+c与y轴的交点坐标为(0,-3),则下列说法不正确的是( )
A.抛物线的开口向上
B.抛物线的对称轴是直线x=1
C.当x=1时,y的最大值为-4
D.抛物线与x轴的交点坐标为(-1,0),(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,-1)和C(4,5)三点.
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值?
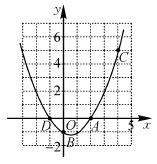
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,排球运动员站在点O处练习发球,将球从O点正上方2 m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m,高度为2.43 m,球场的边界距O点的水平距离为18 m.
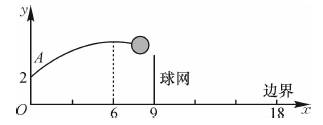
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围);
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com