
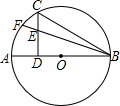
 如图,已知AB是⊙O的直径,CD⊥AB于点D,E是CD上一点,BF交半圆于F.求证:BC2=BE•BF.
如图,已知AB是⊙O的直径,CD⊥AB于点D,E是CD上一点,BF交半圆于F.求证:BC2=BE•BF.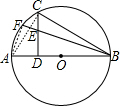 :连结AC,AF,如图,
:连结AC,AF,如图,

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:初中数学 来源: 题型:
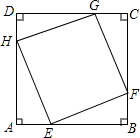 如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.
如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:
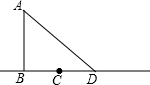 如图,学校旗杆AB的顶端A处挂有一根绳子.小莹在测量旗杆的高度时,先把绳子沿旗杆下垂到点B,固定后再把余下的部分BC拉紧成线段BC(绳子的一端落在C点),然后再将绳子重新拉紧成线段AD(绳子的一端落在D点).小莹只用卷尺在地面上测量了两个数据,就计算出了旗杆高度,你知道测量了哪两个数据吗?你能求出旗杆的高度吗?
如图,学校旗杆AB的顶端A处挂有一根绳子.小莹在测量旗杆的高度时,先把绳子沿旗杆下垂到点B,固定后再把余下的部分BC拉紧成线段BC(绳子的一端落在C点),然后再将绳子重新拉紧成线段AD(绳子的一端落在D点).小莹只用卷尺在地面上测量了两个数据,就计算出了旗杆高度,你知道测量了哪两个数据吗?你能求出旗杆的高度吗?查看答案和解析>>
科目:初中数学 来源: 题型:
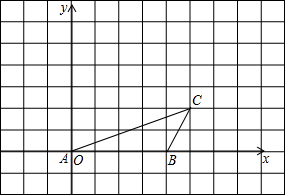 如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com