
分析 已知方程利用拆项法变形后,去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:已知方程整理得:$\frac{1}{2}$($\frac{1}{x}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+4}$+…+$\frac{1}{x+8}$-$\frac{1}{x+10}$)=$\frac{5}{24}$,
即$\frac{1}{x}$-$\frac{1}{x+10}$=$\frac{5}{12}$,
去分母得:12x+120-12x=5x2+50x,即x2+10x-24=0,
分解因式得:(x-2)(x+12)=0,
解得:x1=2,x2=-12,
经检验x1=2,x2=-12都为分式方程的解.
故答案为:x1=2,x2=-12
点评 此题考查了分式方程的解,解题的关键是将已知方程利用拆项法变形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
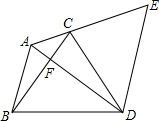 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com