Question

【题目】如图，在Rt△ABC中，∠ABC是直角，AB=3，BC=4，P是BC边上的动点，设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是 ．

Answer 1

【答案】3≤x≤4
【解析】解：过BP中点O，以BP为直径作圆， 连接QO，当QO⊥AC时，QO最短，即BP最短，
∵∠OQC=∠ABC=90°，∠C=∠C，
∴△ABC∽△OQC，
∴ ，
∵AB=3，BC=4，
∴AC=5，
∵BP=x，
∴QO= x，CO=4﹣ x，
∴ ，
解得：x=3，
当P与C重合时，BP=4，
∴BP=x的取值范围是：3≤x≤4，
所以答案是：3≤x≤4．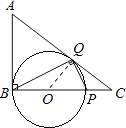

【考点精析】根据题目的已知条件，利用勾股定理的概念和直线与圆的三种位置关系的相关知识可以得到问题的答案，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．