
【题目】问题呈现:
(Ⅰ)如图1,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA上,AE=DG,求证:2S四边形EFGH=S矩形ABCD . (S表示面积)
(Ⅱ)实验探究:某数学实验小组发现:若图1中AH≠BF,点G在CD上移动时,上述结论会发生变化,分别过点E、G作BC边的平行线,再分别过点F、H作AB边的平行线,四条平行线分别相交于点A1、B1、C1、D1 , 得到矩形A1B1C1D1 .
如图2,当AH>BF时,若将点G向点C靠近(DG>AE),经过探索,发现:2S四边形EFGH=S矩形ABCD+S ![]() .
.
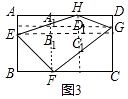
如图3,当AH>BF时,若将点G向点D靠近(DG<AE),请探索S四边形EFGH、S矩形ABCD与S ![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(Ⅲ)迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
⑴如图4,点E、F、G、H分别是面积为25的正方形ABCD各边上的点,已知AH>BF,AE>DG,S四边形EFGH=11,HF= ![]() ,求EG的长.
,求EG的长.
⑵如图5,在矩形ABCD中,AB=3,AD=5,点E、H分别在边AB、AD上,BE=1,DH=2,点F、G分别是边BC、CD上的动点,且FG= ![]() ,连接EF、HG,请直接写出四边形EFGH面积的最大值.
,连接EF、HG,请直接写出四边形EFGH面积的最大值.
【答案】(Ⅰ)证明:如图1中,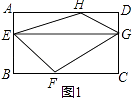
∵四边形ABCD是矩形,
∴AB∥CD,∠A=90°,
∵AE=DG,
∴四边形AEGD是矩形,
∴S△HGE= ![]() S矩形AEGD ,
S矩形AEGD ,
同理S△EGF= ![]() S矩形BEGC ,
S矩形BEGC ,
∴S四边形EFGH=S△HGE+S△EFG= ![]() S矩形ABCD .
S矩形ABCD .
(Ⅱ)实验探究:结论:2S四边形EFGH=S矩形ABCD﹣ ![]() .
.
理由:∵ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴S四边形EFGH= ![]() +
+ ![]() +
+ ![]() +
+ ![]() ﹣
﹣ ![]() ,
,
∴2S四边形EFGH=2 ![]() +2
+2 ![]() +2
+2 ![]() +2
+2 ![]() ﹣2
﹣2 ![]() ,
,
∴2S四边形EFGH=S矩形ABCD﹣ ![]() .
.
(Ⅲ)迁移应用:解:(1)如图4中,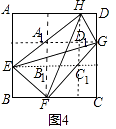
∵2S四边形EFGH=S矩形ABCD﹣ ![]() .
.
∴ ![]() =25﹣2×11=3=A1B1A1D1 ,
=25﹣2×11=3=A1B1A1D1 ,
∵正方形的面积为25,∴边长为5,
∵A1D12=HF2﹣52=29﹣25=4,
∴A1D1=2,A1B1= ![]() ,
,
∴EG2=A1B12+52= ![]() ,
,
∴EG= ![]() .
.
⑵解:∵2S四边形EFGH=S矩形ABCD+ ![]() .
.
∴四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.
①如图5﹣1中,当G与C重合时,四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.
此时矩形A1B1C1D1面积=1( ![]() ﹣2)=
﹣2)= ![]()
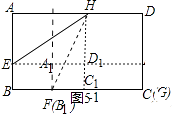
②如图5﹣2中,当G与D重合时,四边形A1B1C1D1面积最大时,矩形EFGH的面积最大.
此时矩形A1B1C1D1面积=21=2,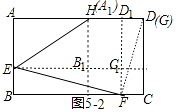
∵2> ![]() ﹣2,
﹣2,
∴矩形EFGH的面积最大值= ![]() .
.
【解析】(Ⅰ)问题呈现:只要证明S△HGE= ![]() S矩形AEGD , 同理S△EGF=
S矩形AEGD , 同理S△EGF= ![]() S矩形BEGC , 由此可得S四边形EFGH=S△HGE+S△EFG=
S矩形BEGC , 由此可得S四边形EFGH=S△HGE+S△EFG= ![]() S矩形BEGC;(Ⅱ)实验探究:结论:2S四边形EFGH=S矩形ABCD﹣
S矩形BEGC;(Ⅱ)实验探究:结论:2S四边形EFGH=S矩形ABCD﹣ ![]() .根据
.根据 ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,即可证明;(Ⅲ)迁移应用:(1)利用探究的结论即可解决问题.(2)分两种情形探究即可解决问题.
,即可证明;(Ⅲ)迁移应用:(1)利用探究的结论即可解决问题.(2)分两种情形探究即可解决问题.
【考点精析】通过灵活运用矩形的性质,掌握矩形的四个角都是直角,矩形的对角线相等即可以解答此题.


科目:初中数学 来源: 题型:
【题目】设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一确定的值和它对应,那么就说y是x的函数,记作y=f(x).在函数y=f(x)中,当自变量x=a时,相应的函数值y可以表示为f(a).
例如:函数f(x)=x2﹣2x﹣3,当x=4时,f(4)=42﹣2×4﹣3=5在平面直角坐标系xOy中,对于函数的零点给出如下定义:
如果函数y=f(x)在a≤x≤b的范围内对应的图象是一条连续不断的曲线,并且f(a).f(b)<0,那么函数y=f(x)在a≤x≤b的范围内有零点,即存在c(a≤c≤b),使f(c)=0,则c叫做这个函数的零点,c也是方程f(x)=0在a≤x≤b范围内的根.
例如:二次函数f(x)=x2﹣2x﹣3的图象如图1所示.
观察可知:f(﹣2)>0,f(1)<0,则f(﹣2).f(1)<0.所以函数f(x)=x2﹣2x﹣3在﹣2≤x≤1范围内有零点.由于f(﹣1)=0,所以,﹣1是f(x)=x2﹣2x﹣3的零点,﹣1也是方程x2﹣2x﹣3=0的根.
(1)观察函数y1=f(x)的图象2,回答下列问题:
①f(a)f(b) 0(“<”“>”或“=”)
②在a≤x≤b范围内y1=f(x)的零点的个数是 .
(2)已知函数y2=f(x)=﹣ ![]() 的零点为x1 , x2 , 且x1<1<x2 .
的零点为x1 , x2 , 且x1<1<x2 .
①求零点为x1 , x2(用a表示);
②在平面直角坐标xOy中,在x轴上A,B两点表示的数是零点x1 , x2 , 点 P为线段AB上的一个动点(P点与A、B两点不重合),在x轴上方作等边△APM和等边△BPN,记线段MN的中点为Q,若a是整数,求抛物线y2的表达式并直接写出线段PQ长的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题原型:如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.过点D作△BCD的BC边上的高DE, 易证△ABC≌△BDE,从而得到△BCD的面积为 ![]() .
.
初步探究:如图②,在Rt△ABC中,∠ACB=90°,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.用含a的代数式表示△BCD的面积,并说明理由.
简单应用:如图③,在等腰三角形ABC中,AB=AC,BC=a.将边AB绕点B顺时针旋转90°得到线段BD,连结CD.直接写出△BCD的面积.(用含a的代数式表示)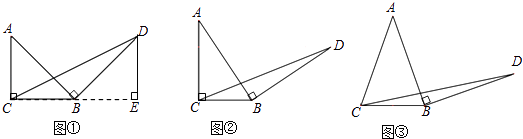
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.
(1)求每张门票的原定票价;
(2)根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F. 
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 . 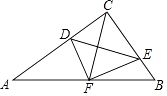
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).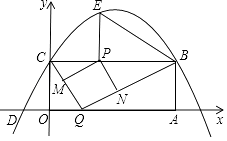
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,洪祥中学开展以“我最喜欢的风景区”为主题的调查活动,围绕“在松峰山、太阳岛、二龙山和凤凰山四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题: 
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若洪祥中学共有1350名学生,请你估计最喜欢太阳岛风景区的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC为⊙O的弦,AB=AC,连接AO.
(1)如图l,求证:∠OAC=∠OAB; 
(2)如图2,过点B作AC的垂线交⊙O于点D,连接CD,设AO的延长线交BD于点E,求证:BE=CD;
(3)在(2)的条件下,如图3,点F,G分别在CD,BD的延长线上,连接AG,AF,若CF×AG=8,∠GAB=45°+ ![]() ∠GAE,∠B=50°,求△ACF的面积.
∠GAE,∠B=50°,求△ACF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com