
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 . 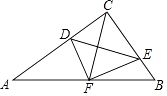
【答案】![]()
【解析】解:由折叠可得,∠DCE=∠DFE=90°, ∴D,C,E,F四点共圆,
∴∠CDE=∠CFE=∠B,
又∵CE=FE,
∴∠CFE=∠FCE,
∴∠B=∠FCE,
∴CF=BF,
同理可得,CF=AF,
∴AF=BF,即F是AB的中点,
∴Rt△ABC中,CF= ![]() AB=5,
AB=5,
由D,C,E,F四点共圆,可得∠DFC=∠DEC,
由∠CDE=∠B,可得∠DEC=∠A,
∴∠DFC=∠A,
又∵∠DCF=∠FCA,
∴△CDF∽△CFA,
∴CF2=CD×CA,即52=CD×8,
∴CD= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】本题主要考查了勾股定理的概念和翻折变换(折叠问题)的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】全球气候变暖导致-些冰川融化并消失,在冰川|消失12年后,一种低等植物苔藓,就开始在岩石上生长,每一个苔藓都会长成近似的圆形,苔藓的直径和其生长年限近似地满足如下的关系式:d=7![]() (t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(t≥12),其中d表示苔藓的直径,单位是厘米,t代表冰川消失的时间(单位:年)。
(1)计算冰川消失16年后苔藓的直径为多少厘米?
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE= ![]() ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 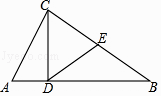
A.60°
B.75°
C.90°
D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,a,b,c分别是ΔABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交AB于D,PE∥AB交AC于E,b,c是方程x2+kx+9=0的两根,且(b2+c2)(b2+c2-14)-72=0,锐角B的正弦值等于![]() 。
。
(1)求K的值;
(2)设BD=x,求四边形ADPE的面积为S关于x的函数关系式;
(3)问圆O是否能与BC相切?若能请求出x的值;若不能,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
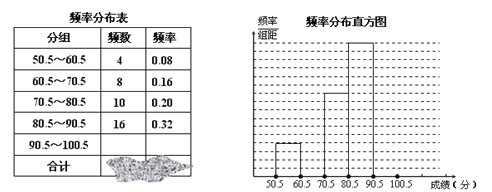
【题目】为了让学生了解环保知识,增强环保意识,红星中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格;
(2)补全频率分布直方图;
(3)在该问题中的样本容量是多少?
答: 。
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)”
答: 。
(5)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
答: 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a≠0,14(a2+b2+c2)=(a+2b+3c)2 , 那么a:b:c=( )
A.2:3:6
B.1:2:3
C.1:3:4
D.1:2:4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com