
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求△ABC的面积.
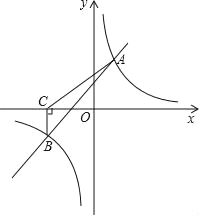
【答案】(1)![]() ,一次函数解析式为y=x+1;(2) 0<x<﹣3或x>2;(3)5.
,一次函数解析式为y=x+1;(2) 0<x<﹣3或x>2;(3)5.
【解析】试题分析:(1)将点A坐标代入反比例函数解析式可得出m的值,继而得出反比例函数解析式,将点B的坐标代入反比例函数解析式可得出n的值,将点A、点B的坐标代入依次函数关系式可得出一次函数的解析式;(2)根据图象直接写出答案即可;(3)求得BC边上的高的长,再利用三角形的面积公式即可求出S△ABC.
试题解析:
(1)∵点A(2,3)在y=mx的图象上,
∴m=6,
∴反比例函数的解析式为:y=![]() ,
,
∵B(3,n)在反比例函数图象上,
∴n=6÷(-3)=2,
∵A(2,3),B(3,2)两点在y=kx+b上,
∴![]()
解得:![]()
∴一次函数的解析式为:y=x+1;
(2)3<x<0或x>2;
(3)以BC为底,则BC边上的高AE为3+2=5,
∴S△ABC=![]() ×2×5=5.
×2×5=5.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
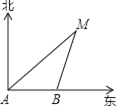
【题目】上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处(如图).从A、B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么在B处船与小岛M的距离为( )
A. 20海里 B. 20![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
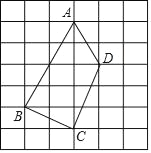
【题目】如图,是大小相等的边长为1的正方形构成的网格,A,B,C,D均为格点.
(Ⅰ)△ACD的面积为_____;
(Ⅱ)现只有无刻度的直尺,请在线段AD上找一点P,并连结BP,使得直线BP将四边形ABCD的面积分为1:2两部分,在图中画出线段BP,并在横线上简要说明你的作图方法._____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
关于x的方程:![]() 的解是
的解是![]() ,
,![]() ;
;![]() 即
即![]() 的解是
的解是![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]() 的解是
的解是![]() ,
,![]() ;
;![]()
![]() 请观察上述方程与解的特征,比较关于x的方程
请观察上述方程与解的特征,比较关于x的方程![]() 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证.
![]() 由上述的观察、比较、猜想、验证,可以得出结论:
由上述的观察、比较、猜想、验证,可以得出结论:
如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
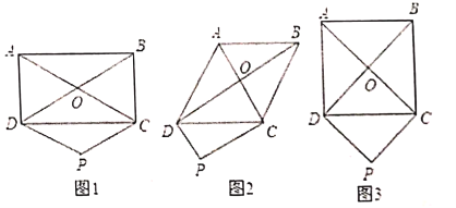
【题目】(1)如图矩形![]() 的对角线
的对角线![]() .
.![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,判断四边形
,判断四边形![]() 的形状并说明理由.
的形状并说明理由.
(2)如果题目中的矩形变为菱形,四边形![]() 的形状____________.
的形状____________.
(3)如果题目中的矩形变为正方形,四边形![]() 的形状____________.
的形状____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.8元,则出售这20筐白菜可卖多少元?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为_____ cm.
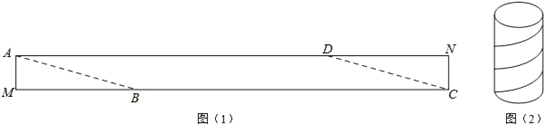
查看答案和解析>>
科目:初中数学 来源: 题型:
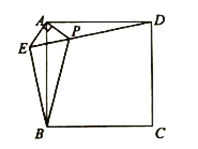
【题目】如图,在正方形![]() 外取一点
外取一点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .过点
.过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() ,其中正确的结论有_____________(填序号)
,其中正确的结论有_____________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
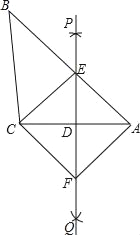
【题目】已知:如图,在△ABC中,直线PQ垂直平分AC,与边AB交于点E,连接CE,过点C作CF∥BA交PQ于点F,连接AF.
(1)求证:四边形AECF是菱形;
(2)若AD=3,AE=5,则求菱形AECF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com