
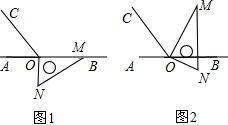
分析 (1)利用角平分线求出∠BOM的度数,又∠MON=90°,所以∠BON=∠MON-∠BOM,即可解答;
(2)设∠COM的余角为x°,则∠COM=(90-x)°,由题意列出方程3x+90-x=120,解出x,即可解答;
(3)利用角的和与差计算.
解答 解:(1)∵∠BOC=120°,OM恰好平分∠BOC,
∴∠BOM=$\frac{1}{2}$∠BOC=60°,
又∵∠MON=90°,
∴∠BON=∠MON-∠BOM=90°-60°=30°.
(2)设∠COM的余角为x°,则∠COM=(90-x)°,
由题意得:3x+90-x=120,
解得:x=15,
3x=45,
所以∠BOM的度数为45°.
(3)∵∠BON=α(0°<α<90°),
∴∠BOM=90°-α,
∴∠COM=120°-∠BOM=120°-(90°-α)=30°+α.
点评 本题考查了有关角的计算,解决本题的关键是观察图形,得出角之间的和与差的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
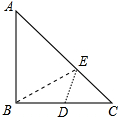 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )
如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是( )| A. | $2\sqrt{5}+2$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{5}$ | D. | $2\sqrt{3}+2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
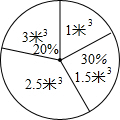 为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:
为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:| 节水量(米3) | 1 | 1.5 | 2.5 | 3 |
| 户数 | a | 90 | 100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
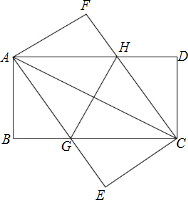 如图所示,已知在矩形ABCD和矩形AECF中,CD=CE,AD与CF相交于点H,BC与AE相交于点G,连接AC、GH.
如图所示,已知在矩形ABCD和矩形AECF中,CD=CE,AD与CF相交于点H,BC与AE相交于点G,连接AC、GH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com