
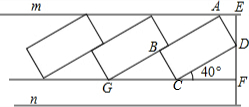
分析 在直角三角形中,利用三角函数关系,由已知角度和边求得ED和DF,而求得EF的长,再在在Rt△BGC中,利用三角函数关系,求得CG的长.
解答 解:由题意知∠DFC=90°,∠DEA=90°,∠DCF=40°
又∵四边形ABCD是矩形,
∴AB=CD=5.4米,BC=AD=2.2米且∠ADC=90°
∵∠DCF+∠CDF=90°且∠ADE+∠CDF=90°
∴∠DCF=∠ADE=40°,
在Rt△DCF中,sin∠DCF=$\frac{DF}{CD}$,
DF=CDsin∠DCF=5.4×sin40°≈5.4×0.64=3.456米,
在Rt△DAE中,COS∠ADE=$\frac{DE}{AD}$,
DE=AD cos∠ADE=2.2×cos40°≈2.2×0.77=1.694米,
EF=DE+DF≈3.456+1.694=5.2米,
∵AG∥CD,
∴∠BGC=DCF=40°,
在Rt△BGC中,sin∠BGC=$\frac{BC}{CG}$,
CG=$\frac{BC}{sin∠BGC}$=$\frac{BC}{sin40°}$=$\frac{2.2}{0.64}$≈3.4米.
∴停车位所占道路的“竖直宽度”EF约为5.2米,“水平宽度”CG约为3.4米.
点评 本题考查了解直角三角形的应用,如何从纷杂的实际问题中整理出直角三角形是解决此类题目的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
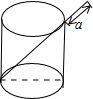 如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是11cm≤a≤12cm.
如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是11cm≤a≤12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:
现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
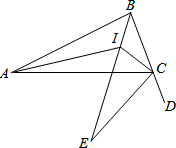 如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.
如图,△ABC中,AI、BI分别平分∠BAC、∠ABC,CE是△ABC的外角∠ACD的平分线,交BI延长线于E,连结CI,若AB=1,且△ABC与△ICE相似,那么AC=$\frac{1}{2}$或1或2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com