
 现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:
现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:分析 (1)将图中框出的16个数相加即可求解;
(2)可设左上角第一个数是x,可得框出的16个数之和为16x+192,令16x+192=2000或2015,求得x为正整数就行,否则就不行.
解答 解:(1)10+11+12+13+17+18+19+20+24+25+26+27+31+32+33+34=44×8=352.
答:图中框出的16个数的和是352.
(2)设左上角一个数是x,则其中最小数为x,最大数为x+31.
依题意有
x+x+7+x+14+x+21+x+1+x+15+x+29+x+43+x+2+x+16+x+30+x+44+x+3+x+17+x+31+x+45=16x+192,
16x+192=2000,
解得x=113.
故框出的16个数之和为2000可能,此时最小值为113,最大值为137;
16x+192=2015,
解得x=113.9375.
故框出的16个数之和2015不可能.
点评 此题考查了一元一次方程的应用,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.


科目:初中数学 来源: 题型:解答题
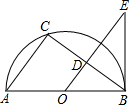 如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.
如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.
如图,正方形AOCB在平面直角坐标系xOy中,点O为原点,点B在反比例函数y=$\frac{k}{x}$(x>0)图象上,△BOC的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,
如图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com