
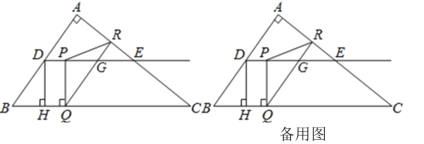
����Ŀ����ͼ����Rt��ABC�У���A=90����AB=6��AC=8��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE�����˶�������P��PQ��BC��Q������Q��QR��BA��AC��R������Q���C�غ�ʱ����Pֹͣ�˶�����BQ=x��QR=y��
(1)���D��BC�ľ���DH�ij���
(2)��y����x�ĺ�����ϵʽ(��Ҫ��д���Ա�����ȡֵ��Χ)��
(3)�Ƿ���ڵ�P��ʹ��PQRΪ����������?�����ڣ��������������Ҫ���x��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��DH=![]() ����2��
����2��![]() ����3�����ڣ�xΪ
����3�����ڣ�xΪ![]() ��
��![]() ��6
��6
��������
��1���������������Ƶ��ж����������BHD�ס�BAC���������������ε��������DH�ij���
��2�����ݡ�RQC�ס�ABC�����������ε����Ʊ����y����x�ĺ�����ϵʽ��
��3������ͼ�Σ�����ͼ�ν������ۣ� PQ��PR�� PQ��RQ�� PR��QR ��
��1����Rt��ABC��
�ߡ�A��90�㣬AB��6��AC��8��
��BC��![]() ��10��
��10��
�ߡ�DHB����A��90�㣬��B����B��
���BHD�ס�BAC��
��![]() ��
��![]() ��
��
��DH��![]() AC��
AC��![]() ��8��
��8��![]()
��2����QR��AB��
���QRC����A��90�㣮
�ߡ�C����C��
���RQC�ס�ABC��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��y����x�ĺ�����ϵʽΪ��y��![]() x+6��
x+6��
��3�����ڣ������������
����PQ��PRʱ������P��PM��QR��M����QM��RM��
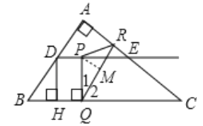
�ߡ�1+��2��90�㣬��C+��2��90�㣬
���1����C��
��cos��1��cosC��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��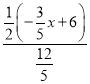 ��
��![]() ��
��
��x��![]() ��
��
����PQ��RQʱ��
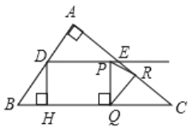
��![]() x+6��
x+6��![]() ��
��
��x��6��
����EM��BC��RN��EM��
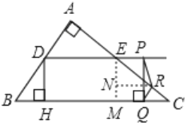
��EM��PQ��
��PR��QRʱ����RΪPQ�д����ϵĵ㣬
��EN��MN��
��ER��RC��
���RΪEC���е㣬
��CR��![]() CE��
CE��![]() AC��2��
AC��2��
��tanC��![]() ��
��![]() ��
��
��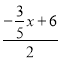 ��
��![]() ��
��
��x��![]() ��
��
������������xΪ![]() ��6��
��6��![]() ʱ����PQRΪ���������Σ�
ʱ����PQRΪ���������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC�Ǿ��Σ��ı���ADEF�������Σ���A��D��x��ĸ������ϣ���C��y����������ϣ���F��AB�ϣ���B��E�ڷ���������y��![]() ��kΪ������k��0����ͼ���ϣ�������ADEF�����Ϊ4����BF��2AF����kֵΪ_____��
��kΪ������k��0����ͼ���ϣ�������ADEF�����Ϊ4����BF��2AF����kֵΪ_____��
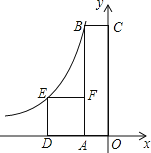
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ������
������![]() ����x�ύ�ڵ�
����x�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��x���ཻ�ڵ�B����ֱ��
��x���ཻ�ڵ�B����ֱ��![]() �ཻ�ڵ�C��
�ཻ�ڵ�C��
��1����ֱ��![]() �ı���ʽ��
�ı���ʽ��
��2��M������Ϊ![]() ����
����![]() ȡ��Сʱ��
ȡ��Сʱ��
����M�����ꣻ
���ᣬ�����궼�������ĵ�������㣮ֱ��д���߶�AM��BM��BC��ACΧ�������ڣ��������߽磩��������꣮
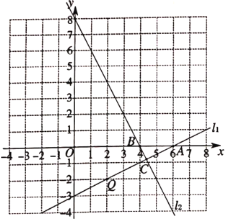
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O���������ABCDE�����Բ�����������εı߳�Ϊa���뾶ΪR�����ľ�Ϊr�������й�ϵʽ������ǣ� ��

A. R2��r2=a2 B. a=2Rsin36�� C. a=2rtan36�� D. r=Rcos36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD�У���֪AD =8���۵�ֽƬʹAB����Խ���AC
�غϣ���B���ڵ�F�����ۺ�ΪAE����EF=3����AB�ij�Ϊ( )

A. 3 B. 4
C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����![]() ��
��![]() �������ͽ���̨�ƹ�
�������ͽ���̨�ƹ�![]() յ��������̨�ƵĽ��ۡ��ۼ������ʾ��
յ��������̨�ƵĽ��ۡ��ۼ������ʾ��

��![]() �����̳�Ԥ�ƽ�����Ϊ
�����̳�Ԥ�ƽ�����Ϊ![]() Ԫ����������̨�Ƹ���������յ��
Ԫ����������̨�Ƹ���������յ��
��![]() �����̳��涨
�����̳��涨![]() ��̨�ƵĽ�������������
��̨�ƵĽ�������������![]() ��̨��������
��̨��������![]() ����Ӧ������������ʹ�̳�������������̨��ʱ������ࣿ��ʱ����Ϊ����Ԫ��
����Ӧ������������ʹ�̳�������������̨��ʱ������ࣿ��ʱ����Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���������Ϊ30Ԫ�������40Ԫ�۳���ƽ��ÿ�����۳�600�����������������������ۼ�ÿ����1Ԫ�����������ͼ���10����
��1��Ϊ��ʹƽ��ÿ����10000Ԫ��������������������ۼ�Ӧ��Ϊ����Ԫ��
��2��10000Ԫ�������Ƿ�Ϊ�����������ǣ���˵�����ɣ�������ǣ�������������ָ����ʱ������ۼ�Ϊ����Ԫ��
��3����������ش��ۼ���ʲô��Χ���̼ҾͿ��Ի������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������ĺ����У��ֱ�װ�г���ɫ����������ͬ��С�����У�����װ��2������1�������Һ���װ��2������1������
��1��������ҡ�Ⱥ����ȡ��һ��С���Ǻ���ĸ�����______��
��2��С����С���̶�������������ҡ�Ⱥ��������һ��С������ɫ��ͬ����С����ʤ������ɫ��ͬ����С����ʤ�������б�������״ͼ�ķ���˵��˭�A�Ŀ����Դ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
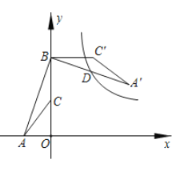
����Ŀ����ͼ����A(-2��0)�� ��B(0��6)��CΪOB���е㣬��![]() �Ƶ�B��ʱ����ת90���õ���A��BC�䣮������������
�Ƶ�B��ʱ����ת90���õ���A��BC�䣮������������![]() ��ͼ��ǡ�þ���A��B���е�D����k��ֵΪ�� ��
��ͼ��ǡ�þ���A��B���е�D����k��ֵΪ�� ��
A.12B.15C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com