
【题目】如图,在平面直角坐标系中,抛物线![]() 交y轴于点B(0,3),交x轴于A,C两点,C点坐标(4,0),点P是BC上方抛物线上一动点(P不与B,C重合).
交y轴于点B(0,3),交x轴于A,C两点,C点坐标(4,0),点P是BC上方抛物线上一动点(P不与B,C重合).
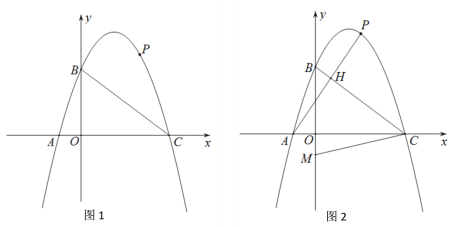
(1)求抛物线的解析式;
(2)若点P到直线BC距离是![]() ,求点P的坐标;
,求点P的坐标;
(3)连接AP交线段BC于点H,点M是y轴负半轴上一点,且CH=BM,当AH+CM的值最小时,请直接写出点M的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)点M坐标(0,
;(3)点M坐标(0,![]() ).
).
【解析】
(1)将点B(4,0),C(0,3)代入原方程得出b、c的值即可求得;
(2)过点P作PE⊥BC于E,则PE=![]() ,过点P作PG∥BC于G,则PG=
,过点P作PG∥BC于G,则PG=![]() ,设P点坐标为
,设P点坐标为![]() ,则G点坐标为
,则G点坐标为![]() ,即PG=
,即PG=![]() ,整理得,
,整理得,![]() ,解得
,解得![]() 或
或![]() ,即可求得点P的坐标;
,即可求得点P的坐标;
(3)在Rt△BOC中,∠BOC=90°,可得BC=5,过点C作CH⊥x轴于N,使CN=BC;连接AN交BC于H交抛物线于点P,则点P即为所求,在射线CB上截取CH=BM,因为CN∥y轴,可得∠NCH=∠CBM,又因为CN=BC,可证△BMC≌△CHN(SAS),即可得到HN=CM,AH+CM=AH+NH,所以当A,N,H三点共线时点P即为所求,AH+CM最小,设AH表达式为![]() ,把A(-1,0),N(4,5)代入上式,求得解析式为y=x+1,联立方程组
,把A(-1,0),N(4,5)代入上式,求得解析式为y=x+1,联立方程组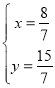 ,解得
,解得![]() ,得到H点坐标是(
,得到H点坐标是(![]() ),CH=BM=
),CH=BM=![]() ,即可得到点M坐标为(0,
,即可得到点M坐标为(0,![]() );
);
(1)把B(4,0),C(0,3)代入原方程得,![]() ,
,
解得:![]() ,
,
∴![]() ;
;
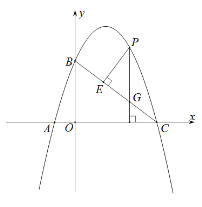
(2)过点P作PE⊥BC于E,则PE=![]() ,
,
过点P作PG∥BC于G,则PG= ,
,
设P点坐标为![]() ,则G点坐标为
,则G点坐标为![]() ,
,
∴PG=![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
∴P![]() ;
;
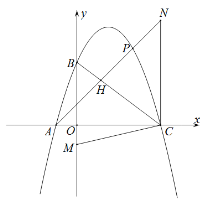
(3)∵在Rt△BOC中,∠BOC=90°,
∴BC=![]() ,
,
过点C作CH⊥x轴于N,使CN=BC;连接AN交BC于H交抛物线于点P,则点P即为所求,
在射线CB上截取CH=BM,
∵CN∥y轴,
∴∠NCH=∠CBM,
∵CN=BC,
∴△BMC≌△CHN(SAS),
∴HN=CM,
∴AH+CM=AH+NH,
∴当A,N,H三点共线时点P即为所求,AH+CM最小,
设AH表达式为![]() ,
,
把A(-1,0),N(4,5)代入上式,
![]() ,
,
解得![]() ,
,
∴y=x+1,
联立方程组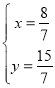
解得![]() ,
,
∴H点坐标是(![]() ),CH=BM=
),CH=BM=![]() ,
,
点M坐标(0,![]() );
);


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:
【题目】“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BD=BC=30m.从A地到D地的距离是( )

A. 30![]() m B. 20
m B. 20![]() m C. 30
m C. 30![]() m D. 15
m D. 15![]() m
m
查看答案和解析>>
科目:初中数学 来源: 题型:
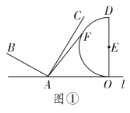
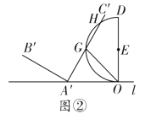
【题目】如图①,已知点![]() 、
、![]() 在直线
在直线![]() 上,且
上,且![]() 于点
于点![]() ,且
,且![]() ,以
,以![]() 为直径在
为直径在![]() 的左侧作半圆
的左侧作半圆![]() 于点
于点![]() ,且
,且![]() .
.
(1)若半圆![]() 上有一点
上有一点![]() ,则
,则![]() 的最大值为__________;
的最大值为__________;
(2)向右沿直线![]() 平移
平移![]() 得到
得到![]() .
.
①如图②,若![]() 截半圆
截半圆![]() 的
的![]() 的长为
的长为![]() ,求
,求![]() 的度数;
的度数;
②当半圆![]() 与
与![]() 的边相切时,求平移距离.
的边相切时,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用1200元购进甲乙两种文具,甲种文具进价12元/个,售价为15元/个.乙种文具进价10元/个,售价为12元/个.全部售完后获利270元.
(1)求该超市购进甲乙两种文具各多少个?
(2)若该超市以原价再次购进这两种文具,且购进甲种文具数量不变,乙种文具购进数量是第一次的2倍,乙种文具按原售价出售,甲种文具降价销售,当两种文具销售完毕后,要使再次购进的文具获利不少于340元,甲种文具每个最低售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
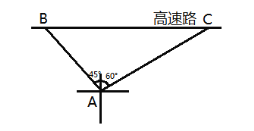
【题目】很多交通事故是由于超速行驶导致的,为集中治理超速现象,高速交警在距离高速路40米的地方设置了一个测速观察点,现测得测速点的西北方向有一辆小型轿车从B处沿西向正东方向行驶,2秒钟后到达测速点北偏东![]() 的方向上的C处,如图.
的方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?
(参考数据:![]() )
)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定速度10%以上不到50%的处200元罚款,扣3分;时速超过限定速度50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/时,你认为该小轿车驾驶员会受到怎样的处罚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,△![]() 的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:

(1)作出△![]() 关于y轴对称的△ A1B1C1,并写出点C1的坐标.
关于y轴对称的△ A1B1C1,并写出点C1的坐标.
(2)以![]() 点为旋转中心,将△
点为旋转中心,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得△ A2B2C2,画出△ A2B2C2 ,并写出点C2的坐标.
得△ A2B2C2,画出△ A2B2C2 ,并写出点C2的坐标.
(3)画出△![]() 关于坐标原点
关于坐标原点![]() 成中心对称的△ A3B3C3,并写出点C3的坐标.
成中心对称的△ A3B3C3,并写出点C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴交于点(-2,0)、(
的图像与x轴交于点(-2,0)、(![]() ),且
),且![]() ,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
,与y轴的正半轴的交点在(0,2)的下方,则下列结论中:①ab>0;②4a-2b+c=0;③2a-b+1<0;④a<b<c,其中正确的结论有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com