Question

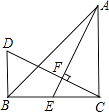
【题目】如图，△ABC中，∠ACB=90°，AC=BC，AE是BC边上的中线，过C作CF⊥AE，垂足为F，过B作BD⊥BC交CF的延长线于D．
（1）求证：AE=CD；
（2）若AC=12cm，求BD的长．

Answer 1

【答案】
（1）证明：∵DB⊥BC，CF⊥AE，

∴∠DCB+∠D=∠DCB+∠AEC=90°．

∴∠D=∠AEC．

又∵∠DBC=∠ECA=90°，

且BC=CA，

在△DBC和△ECA中，

∵

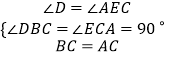
∴△DBC≌△ECA（AAS）．

∴AE=CD

（2）解：由（1）得AE=CD，AC=BC，

在Rt△CDB和Rt△AEC中

，

∴Rt△CDB≌Rt△AEC（HL），

∴BD=CE，

∵AE是BC边上的中线，

∴BD=EC= BC= AC，且AC=12cm．

∴BD=6cm．

【解析】（1）证两条线段相等，通常用全等，本题中的AE和CD分别在三角形AEC和三角形CDB中，在这两个三角形中，已经有一组边相等，一组角相等了，因此只需再找一组角即可利用角角边进行解答．（2）由（1）得BD=EC= BC= AC，且AC=12，即可求出BD的长．
【考点精析】根据题目的已知条件，利用全等三角形的性质的相关知识可以得到问题的答案，需要掌握全等三角形的对应边相等; 全等三角形的对应角相等．