
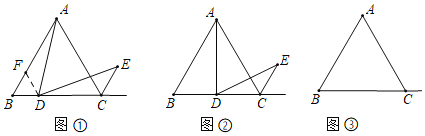
【题目】一节数学课后,老师布置了一道课后练习:△ABC是等边三角形,点D是线段BC上的点,点E为△ABC的外角平分线上一点,且∠ADE=60°,如图①,当点D是线段BC上(除B,C外)任意一点时,求证:AD=DE
(1)理清思路,完成解答
本题证明思路可以用下列框图表:

根据上述思路,请你完整地书写本题的证明过程;
(2)特殊位置,计算求解
当点D为BC的中点时,等边△ABC的边长为6,求出DE的长;
(3)知识迁移,探索新知
当点D在线段BC的延长线上,且满足CD=BC时,若AB=2,请直接写出△ADE的面积(不必写解答过程)
【答案】(1)见解析;(2)3![]() ;(3)3
;(3)3![]() .
.
【解析】
(1)由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(2)解直角三角形求出AD即可解决问题.
(3)只要证明∠BAD=90°,利用勾股定理求出AD,再证明△ADE是等边三角形即可解决问题.
(1)证明:如图①中,过点D作DF∥AC,交AB于点F.
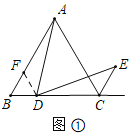
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠BFD=60°,
∴△BDF是等边三角形,BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,
∠DCE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠FAD=∠EDC,
在△AFD≌△DCE中,
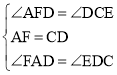 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE.
(2)如图②中,
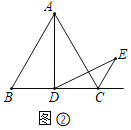
∵△ABC是等边三角形,
∴AB=AC=BC=6,
∵BD=DC=3,
∴AD⊥BC,
∴∠ADB=90°,
∴AD=![]() =3
=3![]() ,
,
由(1)可知:DE=AD=3![]() .
.
(3)如图3中,

∵CA=CD=CB=2,
∴∠BAD=90°,
∴AD=![]() =2
=2![]() ,
,
∵∠ADE=60°,∠ADB=30°,
∴∠BAD=∠EDC=90°,
∵ECD=60°,
∴DE=CDtan60°=2![]() ,
,
∴AD=DE,
∴△ADE是等边三角形,
∴S△ADE=![]() ×(2
×(2![]() )2=3
)2=3![]() .
.


科目:初中数学 来源: 题型:
【题目】2020春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,某校开通了三条人工测体温的通道,每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师),周一有两学生进校园,在3个通道中,可随机选择其中的一个通过.
(1)其中一个学生进校园时,由王老师测体温的概率是_________;
(2)求两学生进校园时,都是王老师测体温的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地,甲车以
地,甲车以![]() 的速度行驶
的速度行驶![]() 后,乙车才沿相同路线行驶,乙车先到达
后,乙车才沿相同路线行驶,乙车先到达![]() 地并停留
地并停留![]() 后,再以原速沿原路返回,直至与甲车相遇.在此过程中,两车之间的距离
后,再以原速沿原路返回,直至与甲车相遇.在此过程中,两车之间的距离![]() 与乙车行驶时间
与乙车行驶时间![]() 之间的函数关系如图所示,下列说法错误的是( )
之间的函数关系如图所示,下列说法错误的是( )
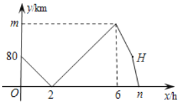
A.乙车的速度是![]() B.
B.![]()
C.点![]() 的坐标是
的坐标是![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由大小相同的黑点按一定规律组成的,第①个图形中有3个黑点第②个图形中有11个黑点,第③个图形中有27个黑点,…,按此规律排列,则第⑦个图形中黑点的个数为( )

A.123B.171C.172D.180
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆是长江上游地区的经济中心、金融中心和创新中心.某公司为了调动员工积极性,将公司员工分成了三个小组进行集分制考核:每月销售业绩第一名集x分,销售业绩第二名集y分,销售业绩第三名集0分(x>y,且均为正整数),经过若干个月(超过4个月)考核后,第一小组集分为23分,第二小组集分为20分,第三小组集分为9分,则第一小组最多得到_____次第二名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校全体学生积极参加献爱心慈善捐款活动,为了解捐款情况,随机抽取了部分学生并对他们的捐款情况作了统计,绘制出两幅不完整的统计图(统计图中每组含最小值,不含最大值).请依据图中信息解答下列问题:
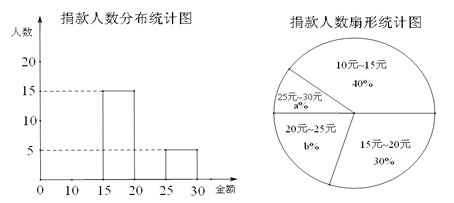
(1)求随机抽取的学生人数;
(2)填空:(直接填答案) ①“20元~25元”部分对应的圆心角度数为 °;
②捐款的中位数落在 .(填金额范围);
(3)若该校共有学生2100人,请估算全校捐款不少于20元的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
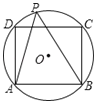
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
小王同学参加某高中学校进行的自主招生考试,本次考试共有1000人参加.
(1)1000人参加自招考试,有300人可以享受加分政策,且有10,20,30,60四个档次,小王想获得至少30分的加分,那么概率为多少?
(2)若该高中的中考录取分数线为530分,小王估得中考分数可能在500-509,510-519,520-529三个分段,
①若小王的中考分数在510~519分段,则小王被该高中录取的概率为多少?
②若小王的中考分数在三个分数段对应的概率分别为![]() ,
,![]() ,
,![]() ,则小王被该高中录取的概率为多少?
,则小王被该高中录取的概率为多少?
加分 | 人数 |
10 | 30 |
20 | 90 |
30 | 150 |
60 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com