
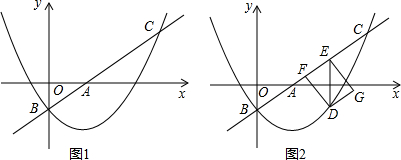
���� ��1���ѵ�B���������ֱ�߽���ʽ���m��ֵ���ٰѵ�C���������ֱ����⼴�ɵõ�n��ֵ��Ȼ�����ô���ϵ��������κ�������ʽ���
��2����y=0�����A�����꣬�Ӷ��õ�OA��OB�ij��ȣ����ù��ɶ�����ʽ���AB�ij���Ȼ�������ֱ��ƽ�У��ڴ�����ȿɵá�ABO=��DEF���ٽ�ֱ����������DE��ʾ��EF��DF�����ݾ��ε��ܳ���ʽ��ʾ��p������ֱ�ߺ������ߵĽ���ʽ��ʾDE�ij����������ɵõ�P��t�Ĺ�ϵʽ�������ö��κ�������ֵ������
��3��������ʱ����ת��Ϊ90��ɵ�B1O1��x��ʱ��A1O1��y��ʱ��Ȼ��֢ٵ�O1��B1����������ʱ����ʾ������ĺ����꣬�ٸ�����������ͬ�г�������⼴�ɣ��ڵ�A1��B1����������ʱ����ʾ����B1�ĺ����꣬�ٸ�����������������A1O1�ij����г�������⼴�ɣ�
��� �⣺��1����ֱ��l��y=$\frac{3}{4}$x+m������B��0��-$\frac{3}{2}$����
��m=-$\frac{3}{2}$��
��ֱ��l�Ľ���ʽΪy=$\frac{3}{4}$x-$\frac{3}{2}$��
��ֱ��l��y=$\frac{3}{4}$x-$\frac{3}{2}$������c��n��$\frac{9}{4}$����
��$\frac{9}{4}$=$\frac{3}{4}$n-$\frac{3}{2}$��
���n=5��
��������y=$\frac{3}{4}$x2+bx+c������C��n��$\frac{9}{4}$���͵�B��0��-$\frac{3}{2}$����
��$\left\{\begin{array}{l}{c=-\frac{3}{2}}\\{\frac{9}{4}=\frac{3}{4}��{5}^{2}+5b+c}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-3}\\{c=-\frac{3}{2}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{3}{4}$x2-3x-$\frac{3}{2}$��
��2����ֱ��l��y=$\frac{3}{4}$x-$\frac{3}{2}$��x�ύ�ڵ�A��
���A��������2��0����
��OA=2��
��Rt��OAB��OB=$\frac{3}{2}$��
��AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+��\frac{3}{2}��^{2}}$=$\frac{5}{2}$��
��DE��y�ᣬ
���OBA=��FED��
�߾���DFEG�У���DFE=90�㣬
���DFE=��AOB=90�㣮
���OAB�ס�FDE��
��$\frac{OA}{FD}$=$\frac{OB}{FE}$=$\frac{AB}{DE}$��
��FD=$\frac{OA}{AB}$•DE=$\frac{4}{5}$DE��
FE=$\frac{OB}{AB}$•DE=$\frac{3}{5}$DE��
��p=2��FD+FE��=2����$\frac{4}{5}$+$\frac{3}{5}$��DE=$\frac{14}{5}$DE��
��D��t��$\frac{3}{4}$t2-3t-$\frac{3}{2}$����E��t��$\frac{3}{4}$t-$\frac{3}{2}$������0��t��5��
��DE=��$\frac{3}{4}$t-$\frac{3}{2}$��-��$\frac{3}{4}$t2-3t-$\frac{3}{2}$��=-$\frac{3}{4}$t2+$\frac{15}{4}$t��
��p=$\frac{14}{5}$����-$\frac{3}{4}$t2+$\frac{15}{4}$t��=-$\frac{21}{10}$t2+$\frac{21}{2}$t��
��p=-$\frac{21}{10}$��t-$\frac{5}{2}$��2+$\frac{105}{8}$����-$\frac{21}{10}$��0��
�൱t=$\frac{5}{2}$ʱ��p�����ֵ$\frac{105}{8}$��
��3����������ɵ�O1B1��x��ƽ�У�O1A1��y��ƽ�У�
1����O1��B1����������ʱ��������������O1��t��y1����B1��t+$\frac{3}{2}$��y1����
��$\frac{3}{4}$t2-3t-$\frac{3}{2}$=$\frac{3}{4}$��t+$\frac{3}{2}$��2-3��t+$\frac{3}{2}$��-$\frac{3}{2}$�����t=$\frac{5}{4}$��
2����A1��B1����������ʱ��������������A1��t��y1����B1��t+$\frac{3}{2}$��y1-2����
��$\frac{3}{4}$t2-3t-$\frac{3}{2}$=$\frac{3}{4}$��t+$\frac{3}{2}$��2-3��t+$\frac{3}{2}$��-$\frac{3}{2}$+2�����t=$\frac{13}{36}$��
���ϣ���A1�ĺ�����Ϊ$\frac{5}{4}$��$\frac{13}{36}$��
���� �����Ƕ��κ����ۺ����ͣ���Ҫ������һ�κ���ͼ���ϵ����������������ϵ��������κ�������ʽ��������Ǻ����������ε��ܳ���ʽ���Լ����κ�������ֵ���⣬�����ѵ����ڣ�3��������ת����90���жϳ�B1O1��x��ʱ��A1O1��y��ʱ��ע��Ҫ��������ۣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
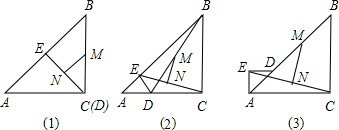
 ��ͼ���ڳ�����ABCD�У���֪AB=8cm��BC=10cm����AD��ֱ��AF�۵���ʹ��D����BC�ĵ�E������CF�ij���
��ͼ���ڳ�����ABCD�У���֪AB=8cm��BC=10cm����AD��ֱ��AF�۵���ʹ��D����BC�ĵ�E������CF�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$��$\sqrt{3}$=$\sqrt{6}$ | B�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C�� | $\sqrt{8}$=4$\sqrt{2}$ | D�� | $\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �״�M�س���ȥN�أ��Ҵ�ı㳵Ҳ��M�س�����;����M��N������ͬһ��ֱ���ϵ�G�أ�����N��ͣ��һ��ʱ�����110km/h���ٶȷ��أ�����G��ͣ����$\frac{3}{4}$h��ͽ������M�أ�����5kmʱ�뷵�صļ���������׳�����M�أ���ͼ��������M�صľ���y����λ��km�����н�ʱ��x����λ��h��֮��ĺ���ͼ�ס��Ҿ������н����������������أ���
�״�M�س���ȥN�أ��Ҵ�ı㳵Ҳ��M�س�����;����M��N������ͬһ��ֱ���ϵ�G�أ�����N��ͣ��һ��ʱ�����110km/h���ٶȷ��أ�����G��ͣ����$\frac{3}{4}$h��ͽ������M�أ�����5kmʱ�뷵�صļ���������׳�����M�أ���ͼ��������M�صľ���y����λ��km�����н�ʱ��x����λ��h��֮��ĺ���ͼ�ס��Ҿ������н����������������أ����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com