
����Ŀ��������⣺��ͼ1�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽���DC���E����֤��PB=PE
�������⣺ѧ���ף���ͼ1������P��PM��BC��PN��CD������ֱ�ΪM��Nͨ��֤����������ȫ�ȣ�����֤�������߶���ȣ�
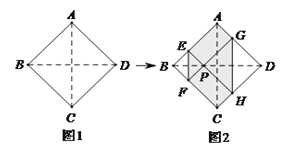
ѧ���ң�����DP����ͼ2��������֤��PD=PB��Ȼ����ͨ�����ȽǶԵȱ���֤��PE=PD���Ϳ���֤��PB=PE�ˣ�
������⣺����ѡ������һ�ַ�������֤����
�������죺��ͼ3���ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��PB=PE������������������֤����������������˵�����ɣ�

���𰸡�������⣺֤�����������������죺������֤��������.
���������������������ͼ1�����������ε����ʵ���BCD=90����ACƽ����BCD����PM��BC��PN��CD�����ı�PMCNΪ���Σ����ݽ�ƽ�������ʵ�PM=PN�������ı����ڽǺ͵õ���PBC+��CEP=180���������õȽǵIJ�����ȵõ���PBM=��PEN��Ȼ�������AAS��֤����PBM�ա�PEN����PB=PE��
����ͼ2������PD�����������ε����ʵ�CB=CD��CAƽ����BCD�����ݽ�ƽ���ߵ����ʵ���BCP=��DCP���ٸ�����SAS��֤����CBP�ա�CDP����PB=PD����CBP=��CDP�������ı����ڽǺ͵õ���PBC+��CEP=180���������õȽǵIJ�����ȵõ���PBC=��PED������PED=��PDE������PD=PE�����ǵõ�PB=PD��
����ͼ3������P��PM��BC��PN��CD������ֱ�ΪM��N�����������ε����ʵ���BCD=90����ACƽ����BCD����PM��BC��PN��CD���õ��ı�PMCNΪ���Σ�PM=PN������MPN=90�������õȽǵ������ȵõ���BPM=��EPN��Ȼ�������AAS��֤����PBM�ա�PEN������PB=PE��
���������֤������ͼ1��
���ı���ABCDΪ�����Σ�
���BCD=90����ACƽ����BCD��
��PM��BC��PN��CD��
���ı�PMCNΪ���Σ�PM=PN��
�ߡ�BPE=90������BCD=90����
���PBC+��CEP=180����
����CEP+��PEN=180����
���PBM=��PEN��
����PBM����PEN��

���PBM�ա�PEN��AAS����
��PB=PE��
��ͼ2������PD��

���ı���ABCDΪ�����Σ�
��CB=CD��CAƽ����BCD��
���BCP=��DCP��
����CBP����CDP��
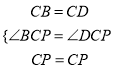 ��
��
���CBP�ա�CDP��SAS����
��PB=PD����CBP=��CDP��
�ߡ�BPE=90������BCD=90����
���PBC+��CEP=180����
����CEP+��PEN=180����
���PBC=��PED��
���PED=��PDE��
��PD=PE��
��PB=PD��
��ͼ3��PB=PE��������

�������£�����P��PM��BC��PN��CD������ֱ�ΪM��N��
���ı���ABCDΪ�����Σ�
���BCD=90����ACƽ����BCD��
��PM��BC��PN��CD��
���ı�PMCNΪ���Σ�PM=PN��
���MPN=90����
�ߡ�BPE=90������BCD=90����
���BPM+��MPE=90����
����MEP+��EPN=90����
���BPM=��EPN��
����PBM����PEN��
 ��
��
���PBM�ա�PEN��AAS����
��PB=PE��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������ֽƬABCD�ı߳�Ϊ2��������B����D��ʹ������ֱ�ǵĶ����غ��ڶԽ���BD��һ��P��EF��GH�ֱ����ۺۣ���ͼ2������AE��x��0��x��2�������������жϣ�
����x��1ʱ����P��������ABCD�����ģ�
����x��![]() ʱ��EF��GH��AC��
ʱ��EF��GH��AC��
����0��x��2ʱ��������AEFCHG��������ֵ��![]() ��
��
����0��x��2ʱ��������AEFCHG�ܳ���ֵ���䣮
������ȷ����________������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʮһ�ƽ����ڼ䣬��կ��7����ÿ�����������ı仯������±���������ʾ��9��30�ն��������������ʾ��9��30���ٵ���������
���� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯/���� | +0.5 | +0.7 | +0.8 |
|
| +0.2 |
|
(1)�����ж�7�����ο��������������ٵĸ�����һ�죿�������������ˣ���5�֣�
(2)�����9��30����������Ϊ2.5���ˣ�ƽ��ÿ������500Ԫ�����ʷ羰���ڴ�7����������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����У��ں���y=2x��3ͼ���ϵĵ��ǣ� ��
A.��0��0��
B.��1����1��
C.��1��1��
D.����1��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���y=![]() x+b��ͼ���뷴��������y=
x+b��ͼ���뷴��������y=![]() ��x��0����ͼ���ڵ�A����1��2���͵�B����C��y���ϣ�
��x��0����ͼ���ڵ�A����1��2���͵�B����C��y���ϣ�
��1������ABC���ܳ���Сʱ�����C�����ꣻ
��2����![]() x+b��
x+b��![]() ʱ����ֱ��д��x��ȡֵ��Χ��
ʱ����ֱ��д��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�����2017���п���ѧѧ�Ƹ������γɼ��ֲ���������г�ȡ150���������п���ѧ�ɼ�����ͳ�Ʒ���������������У�������ָ�� ��
A.150
B.����ȡ��150������
C.����ȡ��150���������п���ѧ�ɼ�
D.����2013���п���ѧ�ɼ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com