
【题目】阅读下面内容,并解决问题:
《名画》中的数学
前苏联著名科学家别莱利曼在他所著的《趣味代数学》中介绍了波格达诺夫·别列斯基的《名画》,画上那位老师拉金斯基是一位自然科学教授,放弃了大学教席(教师职务)来到农村学校当一名普通老师.画中,黑板上写着一道式子,如图所示:

从这道算式计算可以得出答案等于2,如果仔细一研究,10,11,12,13,14这几个数具有一种有趣的特性:![]() ,而且
,而且![]() .
.
请解答以下问题:
(1)还有没有其他像这样五个连续的整数,前三个数的平方和正好等于后两个数的平方和呢?如果有,请求出另外的五个连续的整数;
(2)若七个连续整数前四个数的平方和等于后三个数的平方和,请直接写出符合条件的连续整数.
【答案】(1)存在其他五个连续的整数-2,-1,0,1,2,前三个数的平方和正好等于后两个数的平方和;(2)21,22,23,24,25,26,27和-3,-2,-1,0,1,2,3.
【解析】
(1)设五个连续整数为n,n+1,n+2,n+3,n+4,根据题意n2+(n+1)2+(n+2)2=(n+3)2+(n+4)2,解方程得到n.
(2)设七个连续整数为n-3,n-2,n-1,n,n+1,n+2,n+3,根据题意(n-1)2+(n-2)2++(n-3)2+n2=(n+1)2+(n+2)2+(n+3)2,解方程得到n.
(1)存在其他像这样五个连续的整数,前三个数的平方和正好等于后两个数的平方和.
设x为这五个连续整数的第二个数.
依题意列方程,得![]() .
.
化简,得![]() .
.
解这个方程,得![]() ,
,![]() ,
,
∴五个连续的整数为10,11,12,13,14和-2,-1,0,1,2,前三个数的平方和正好等于后两个数的平方和.
答:存在其他五个连续的整数-2,-1,0,1,2,前三个数的平方和正好等于后两个数的平方和.
(2)设七个连续整数为n-3,n-2,n-1,n,n+1,n+2,n+3,根据题意得:
(n-1)2+(n-2)2+(n-3)2+n2=(n+1)2+(n+2)2+(n+3)2,
∴n2-24n=0
解得n=24或n=0,
当n=24时这五个数为21,22,23,24,25,26,27.
当n=0时这五个数为-3,-2,-1,0,1,2,3.
故答案为:符合条件的连续整数有两组:
第一组21,22,23,24,25,26,27;
第二组-3,-2,-1,0,1,2,3.


科目:初中数学 来源: 题型:
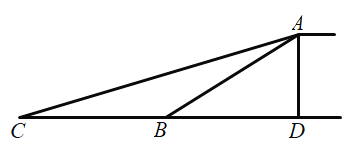
【题目】某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯![]() 长为
长为![]() ,坡角
,坡角![]() 为
为![]() ”改造后的斜坡式自动扶梯的坡角
”改造后的斜坡式自动扶梯的坡角![]() 为
为![]() ,若国标规定自动扶梯的速度一般是
,若国标规定自动扶梯的速度一般是![]() ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:
,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据:![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
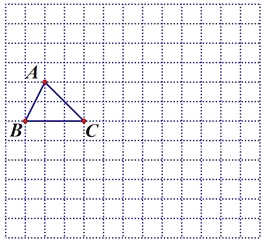
【题目】如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度后得到△A1B1C1.画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2.画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在美化校园的活动中,数学兴趣小组用16m长的篱笆,一边靠墙围成一个矩形花园ABCD,墙长为6m,设AB![]() m.
m.
(1)若花园的面积为14![]() ,求
,求![]() 的值;
的值;
(2)花园的面积能否为40![]() ?为什么?
?为什么?
(3)若要求花园的面积大于24![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料,再解答问题:
已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.例如:求点
计算.例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:由直线![]() 可知:
可知:![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]()
![]() .
.
求:(1)已知直线![]() 与
与![]() 平行,求这两条平行线之间的距离;
平行,求这两条平行线之间的距离;
(2)已知直线![]() 分别交
分别交![]() 轴于
轴于![]() 两点,
两点,![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 为
为![]() 上的动点,试求
上的动点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
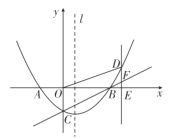
如图,抛物线![]() ,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作![]() 轴于点E,交直线BC于点F,当
轴于点E,交直线BC于点F,当![]() 时,求四边形DOBF的面积;
时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“足球运球”是中考体育必考项目之一.我市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A、B、C、D四个等级进行统计,制成了如图不完整的统计图.
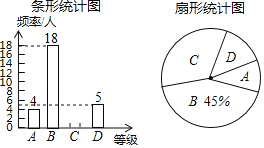
根据所给信息,解答以下问题:
(1)本次抽样调查抽取了 名学生的成绩;在扇形统计图中,D对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
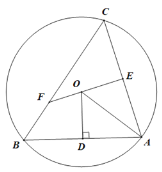
【题目】如图所示,△ABC是圆O的内接三角形,过点O作OD⊥AB与点D,连接OA,点E是AC的中点,延长EO交BC于点F.
(1)求证:△CEF∽△ODA.
(2)若![]() ,△ABC是不是等腰三角形?并说明理由.
,△ABC是不是等腰三角形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com