
分析 (1)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(4)方程去分母,移项合并,把x系数化为1,即可求出解;
(5)方程去分母,移项合并,把x系数化为1,即可求出解;
(6)方程去分母,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去分母得:2x-12=20x+1,
移项合并得:18x=-13,
解得:x=-$\frac{13}{18}$;
(2)去括号得:3x-3+2=2x+6+7,
移项合并得:x=14;
(3)去分母得:x-1=-2x-6+3,
移项合并得:3x=-2,
解得:x=-$\frac{2}{3}$;
(4)去分母得:25x+x=260,
合并得:26x=260,
解得:x=10;
(5)去分母得:10(x-6)=15-6(x+2),
去括号得:10x-60=15-6x-12,
移项合并得:16x=63,
解得:x=$\frac{63}{16}$;
(6)去分母得:20-5(x-1)=2(x+2),
去括号得:20-5x+5=2x+4,
移项合并得:7x=21,
解得:x=3.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
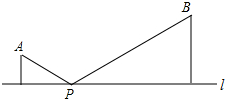 如图,点A,B都在直线l的同一侧,若P为直线l上一点,且满足PA+PB最短为点A到直线l的距离与点B到直线L的距离之和的2倍,则∠APB=120度.
如图,点A,B都在直线l的同一侧,若P为直线l上一点,且满足PA+PB最短为点A到直线l的距离与点B到直线L的距离之和的2倍,则∠APB=120度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
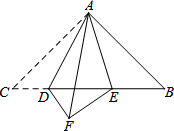 已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com