
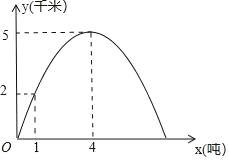
【题目】根据对宁波市相关的市场物价调研,某批发市场内甲种水果的销售利润y1(千元)与进货量x(吨)近似满足函数关系y1=0.25x,乙种水果的销售利润y2(千元)与进货量x(吨)之间的函数y2=ax2+bx+c的图象如图所示.
(1)求出y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种水果共8吨,设乙水果的进货量为t吨,写出这两种水果所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
科目:初中数学 来源: 题型:
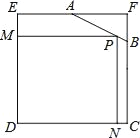
【题目】已知边长为4的正方形截去一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.当P在AB上运动时,矩形PNDM的最大面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”是中华民族每一个人的梦,也是每一个中小学生的梦,各中小学开展经典诵读活动,无疑是“中国梦”教育这一宏大乐章里的响亮音符,学校在经典诵读活动中,对全校学生用A、B、C、D四个等级进行评价,现从中抽取若干个学生进行调查,绘制出了两幅不完整的统计图,请你根据图中信息解答下列问题:
(1)共抽取了多少个学生进行调查?
(2)将图甲中的折线统计图补充完整.
(3)求出图乙中B等级所占圆心角的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
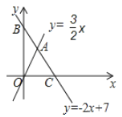
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 点坐标;
点坐标;
(2)如果在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 点坐标;
点坐标;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于6?若存在,请求出
的面积等于6?若存在,请求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶,图②是客车、货车离 C站的路程![]() 、
、![]() (km)与行驶时间x(h)之间的函数图像.
(km)与行驶时间x(h)之间的函数图像.

(1)客车的速度是 km/h;
(2)求货车由 B地行驶至 A地所用的时间;
(3)求点E的坐标,并解释点 E的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数的图象经过点A(2,4)和B(﹣1,﹣5)两点.
(1)求出该一次函数的表达式;
(2)画出该一次函数的图象;
(3)判断(﹣5,﹣4)是否在这个函数的图象上?
(4)求出该函数图象与坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣4,2),B(﹣2,4),C(﹣4,4),以原点O为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,﹣2),则点A的对应点A′的坐标为( )

A. (2,﹣3) B. (2,﹣1) C. (3,﹣2) D. (1,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
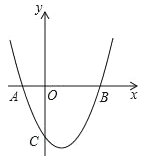
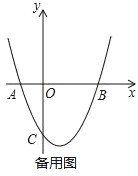
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.
(1)求抛物线的表达式;
(2)抛物线上有两点M(x1,y1)和N(x2,y2),若x1<1,x2>1,x1+x2>2,试判断y1与y2的大小,并说明理由;
(3)平移该抛物线,使平移后的抛物线经过点O,且与x轴交于点D,记平移后的抛物线顶点为点P
①若△ODP是等腰直角三角形,求点P的坐标;
②在①的条件下,直线x=m(0<m<3)分别交线段BP、BC于点E、F,且△BEF的面积:△BPC的面积=2:3,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.

(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求PAC为直角三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com